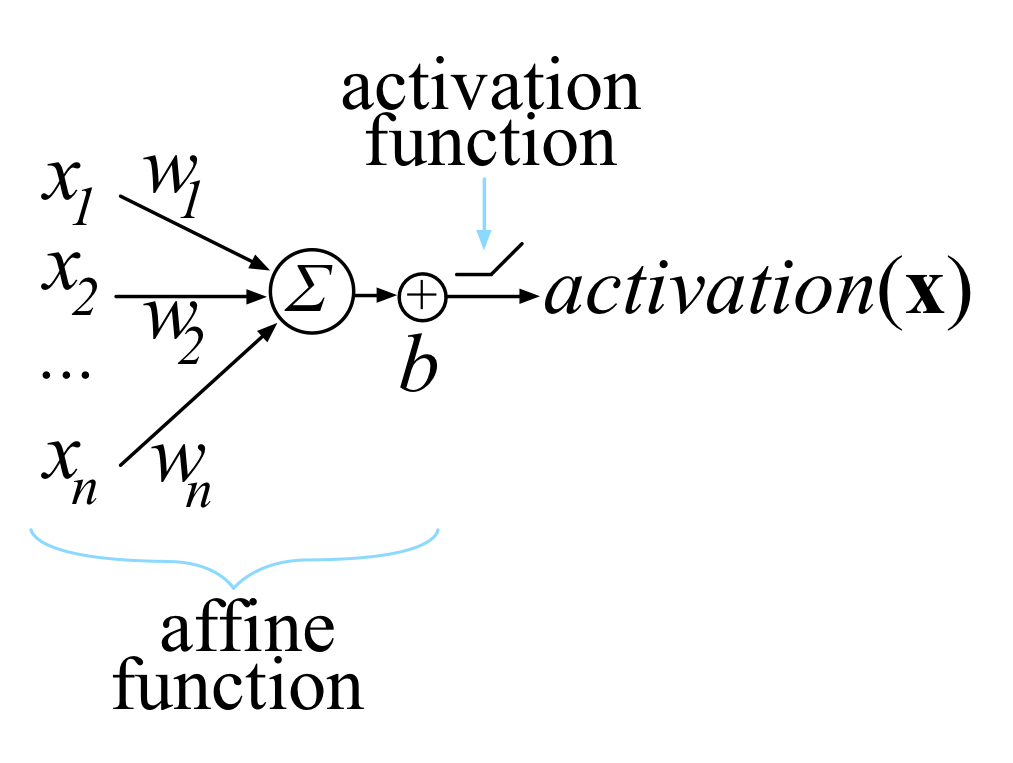
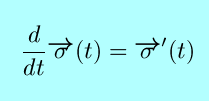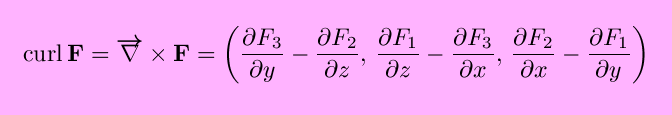Vector Calculus Summary

A b g t d t g b g a.

Vector calculus summary. We also give some of the basic properties of vector arithmetic and introduce the common i j k notation for vectors. Look at any points where fisnt differentiable. The divergence of this vector field is defined as. Divergence of a vector field and gauss theorem consider a three dimensional vector field defined by f p q r where p q and r are all functions of x y and z.

Vector calculus summary vectors. The derivative unit tangent vector and arc length. The term vector calculus is sometimes used as a synonym for the broader subject of multivariable calculus which includes vector calculus as well as partial differentiation and multiple integration. Vector arithmetic in this section we will discuss the mathematical and geometric interpretation of the sum and difference of two vectors.

Vector fields and line integrals in the plane. Fis conservative if there is a scalar function such that f that is the vector eld is the gradient of some scalar function f hmnpi is conservative if and only if m x n y p. Vector calculus plays an important role in differential geometry and in the study of partial differential equations. Specifically the divergence of a vector is a scalar.

Vector calculus or vector analysis is a branch of mathematics concerned with differentiation and integration of vector fields. We also define and give a geometric interpretation for scalar multiplication. Path independence and conservative. Double integrals and line integrals in the plane.

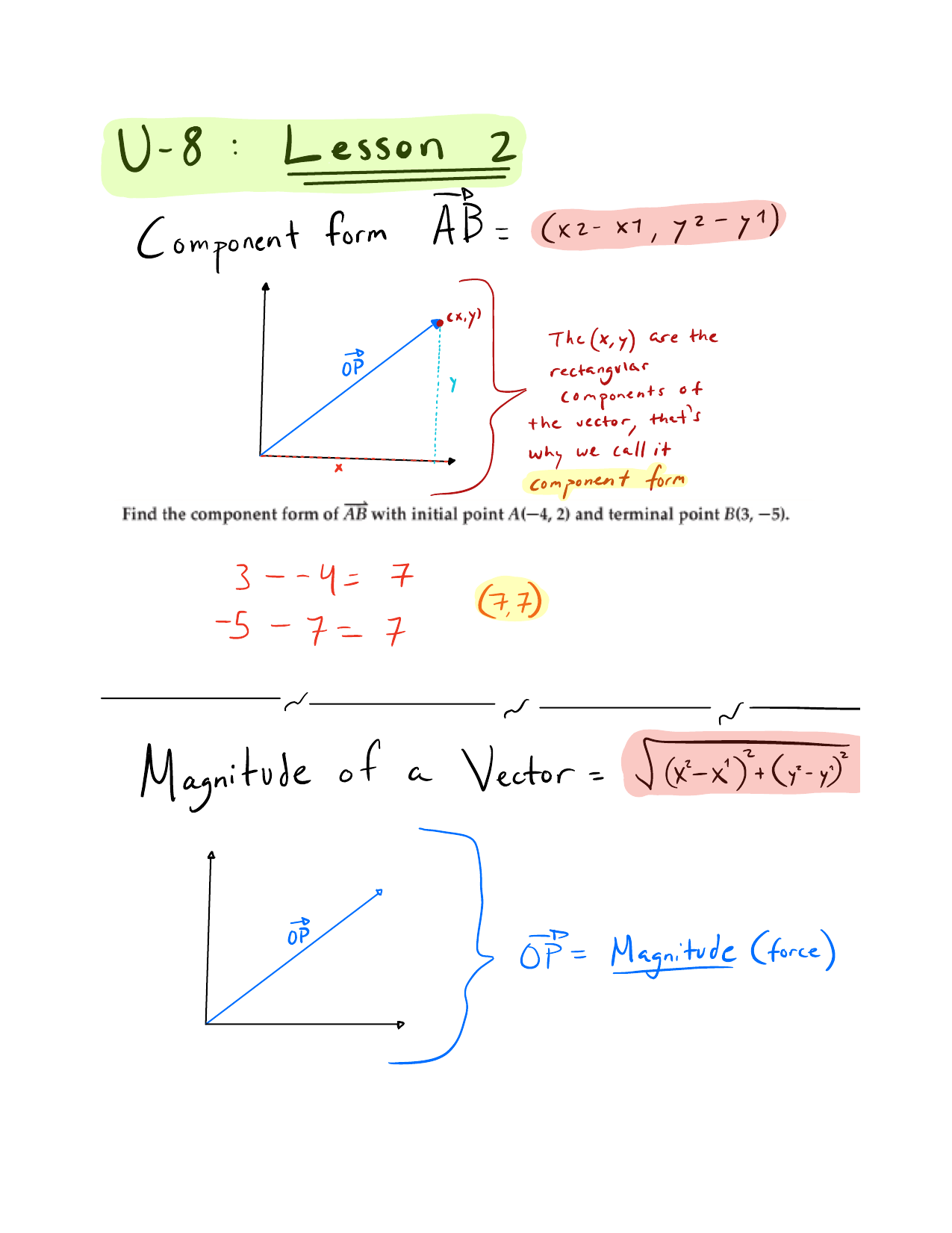
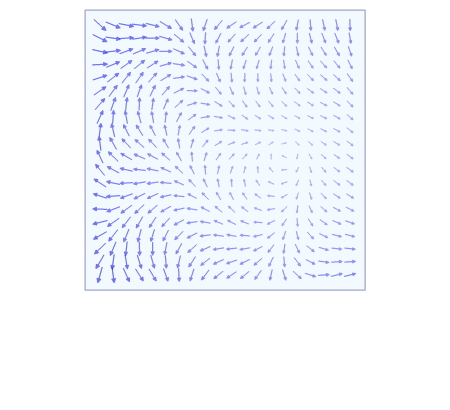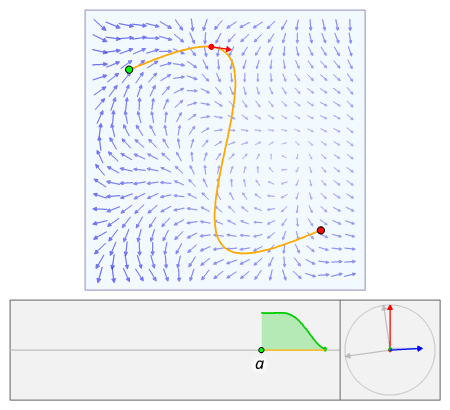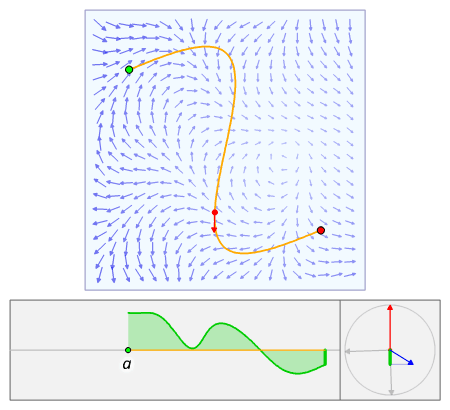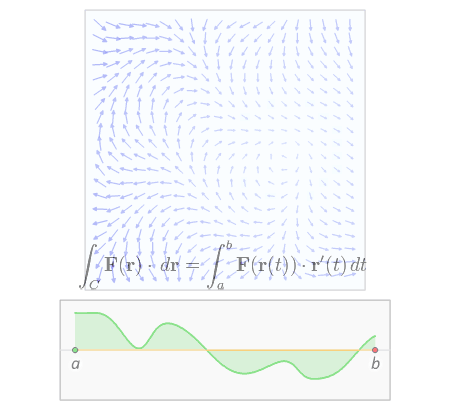
The fundamnetal theorem of calculus equates the integral of the derivative g t to the values of g t at the interval boundary points. Diverge. Look at the boundary of d. Week 6 summary.

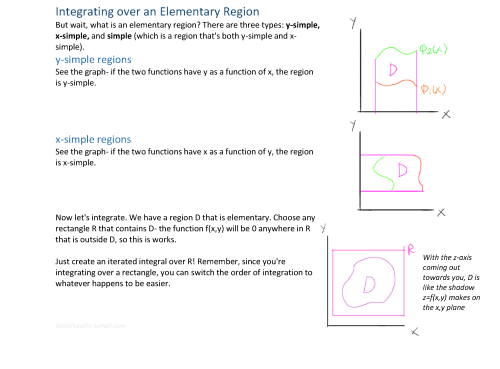
Maximization and minimization of functions of two variables. Change of variables for multiple integrals. The divergence of a higher order tensor field may be found by decomposing the tensor field into a sum of outer products and using the identity. It is used extensively in physics and engineering especially in the description of electromagnetic fields gravitational fields and fluid flow.

Vectors make it easier to describe our favorite geometric objects. Week 7 summary. Week 8 summary. Gradients and directional derivatives.

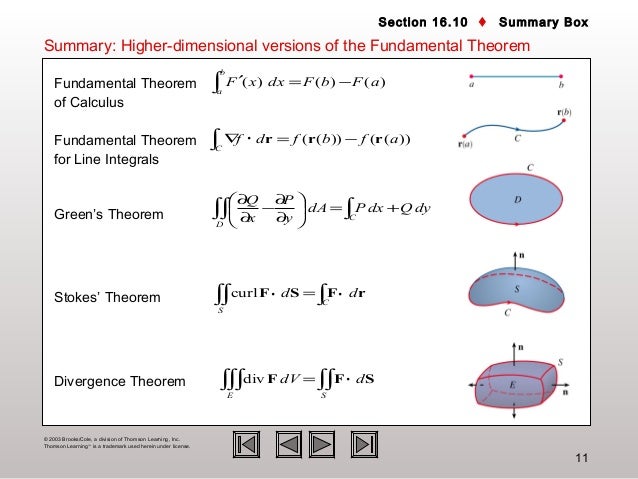
A typical vector field for example would be f 2x xy z 2 x. The four fundamental theorems of vector calculus are generalizations of the fundamental theorem of calculus. Vector calculus at a glance.