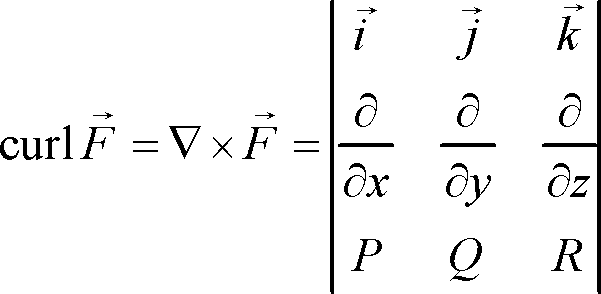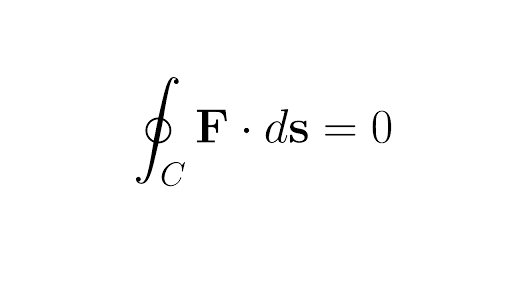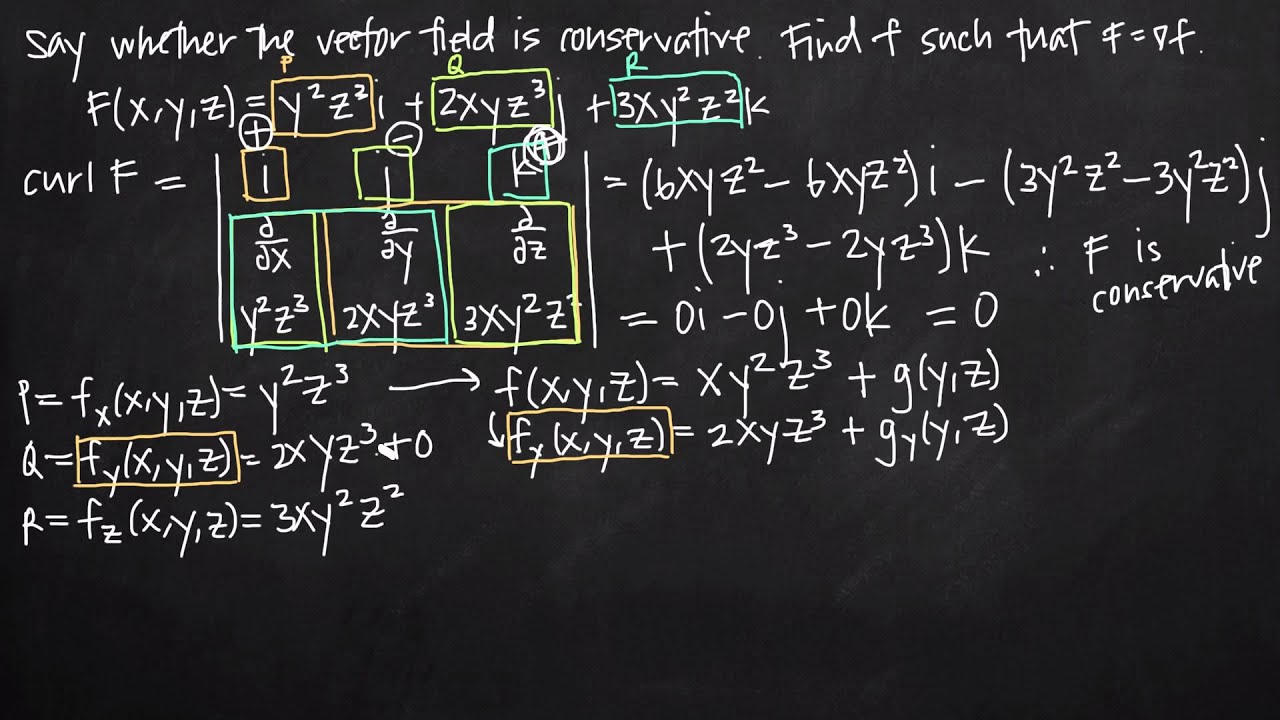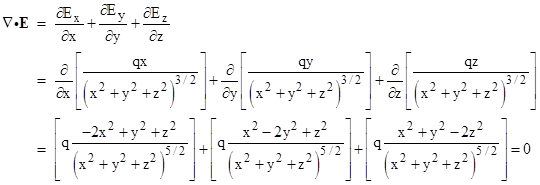Conservative Vector Field Curl

A conservative vector field is also irrotational. Conservative vector fields in the previous section we saw that if we knew that the vector field f f was conservative then c f dr c f d r was independent of path. Conservative vector fields have the property that the line integral is path independent.
conservative vector field curl conservative vector field curl is zero

The gradient theorem for line integrals.

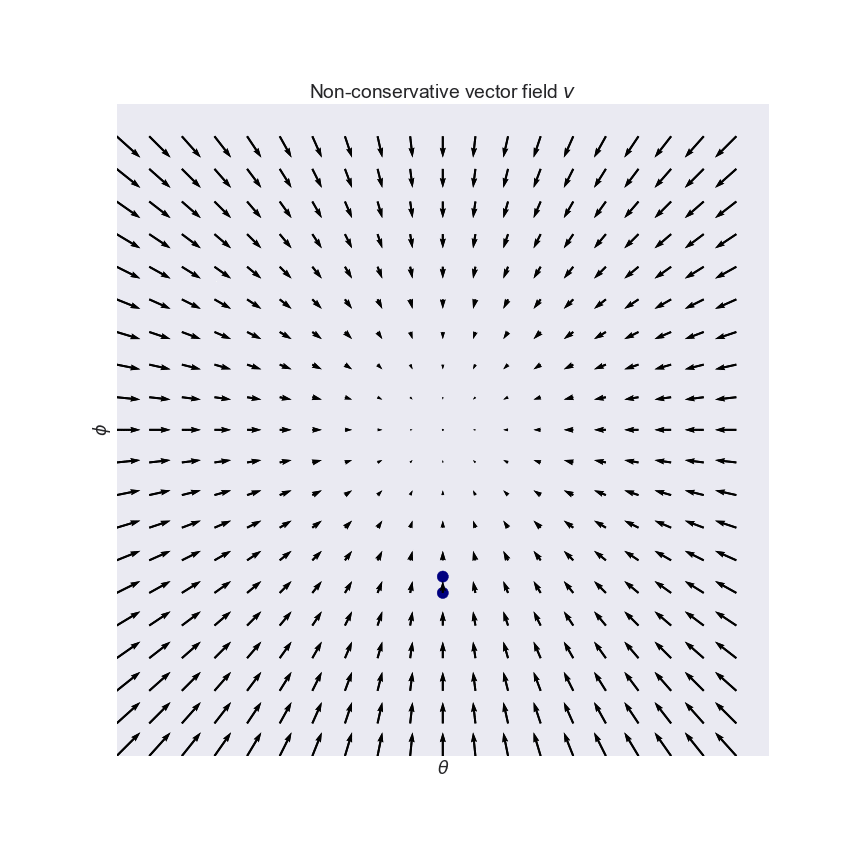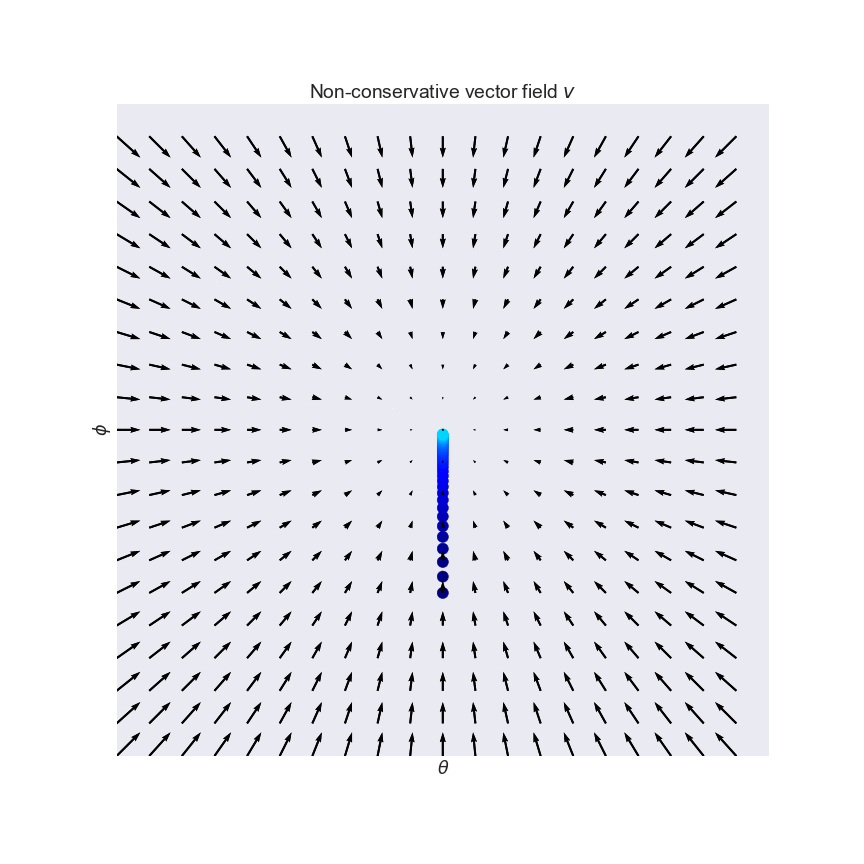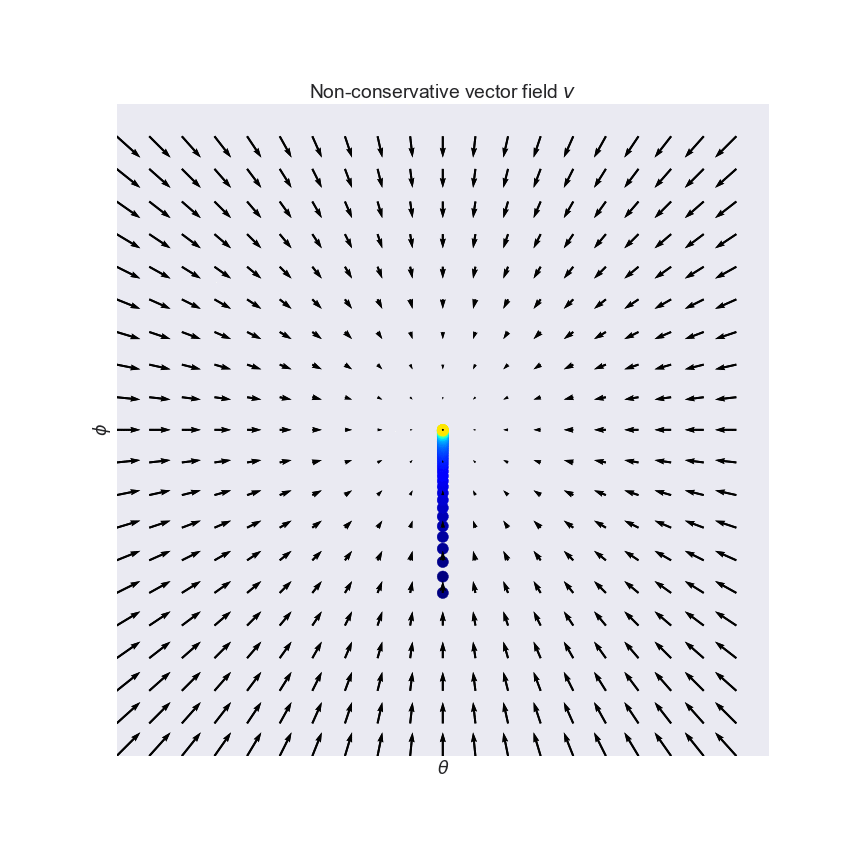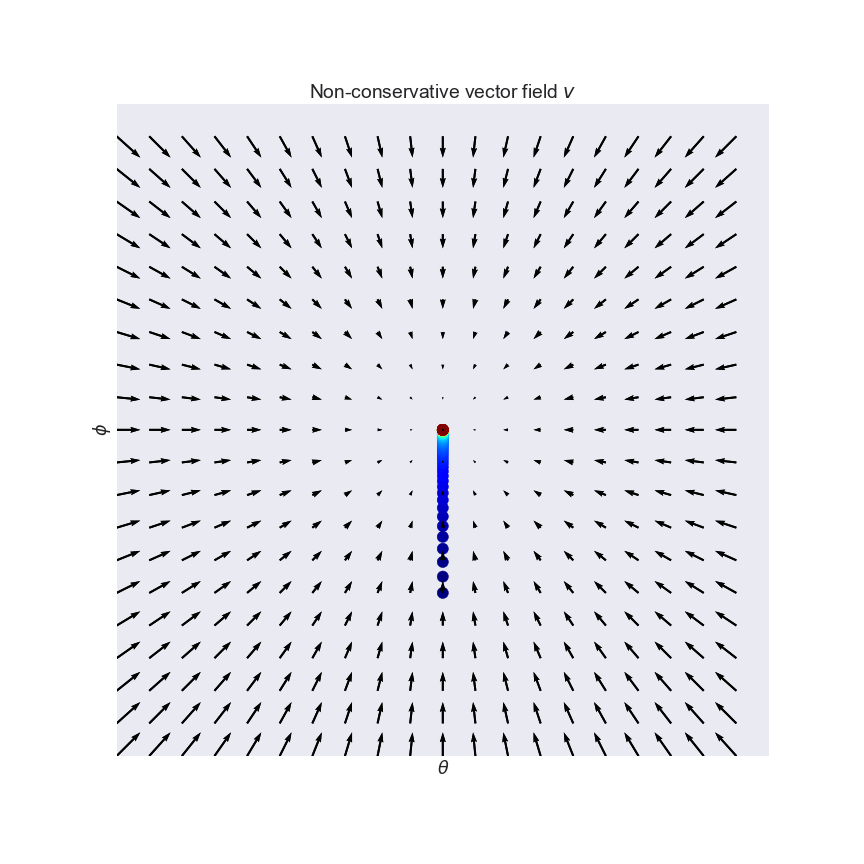
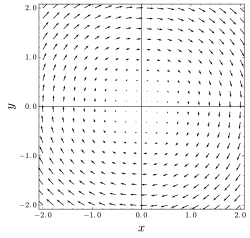
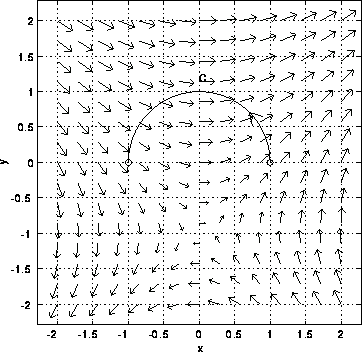
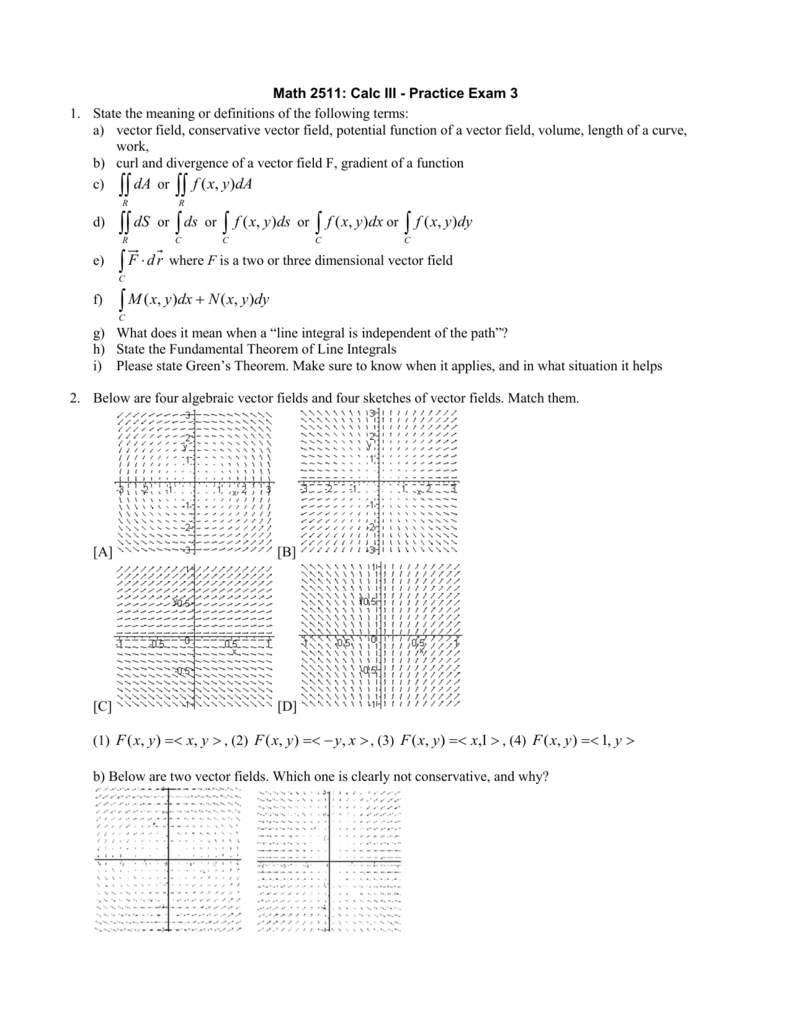
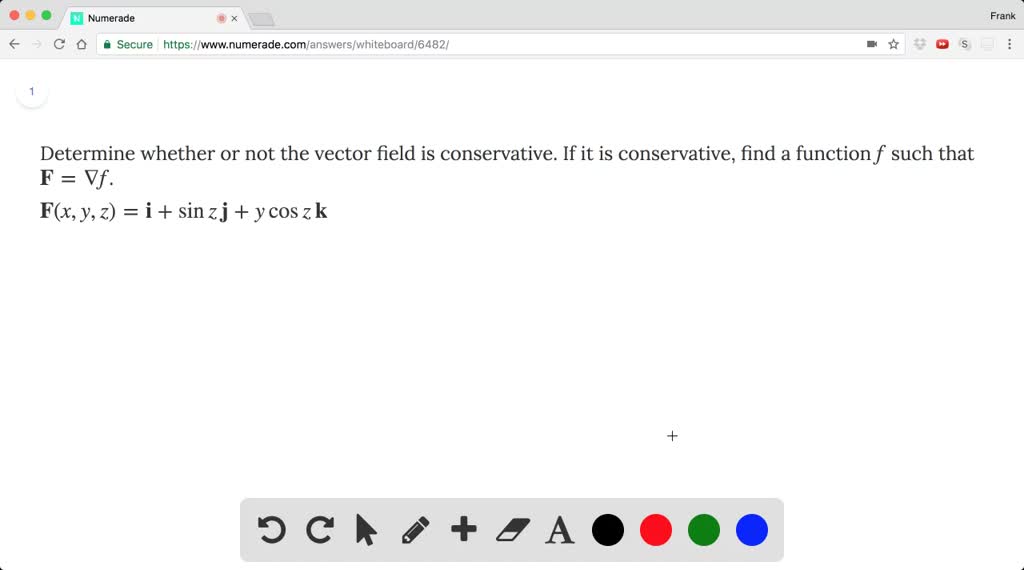
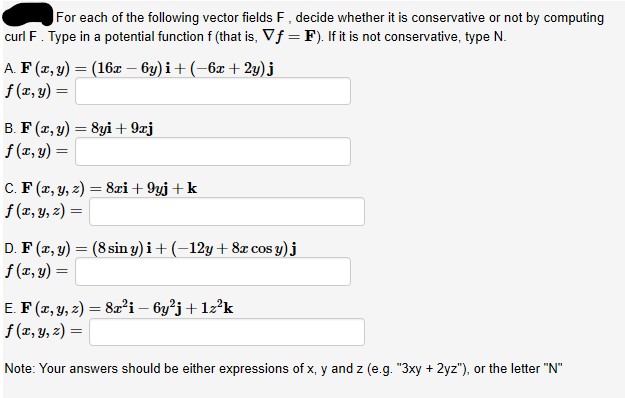
Conservative vector field curl. The choice of any path between two points does not change the value of the line integral. The curl of a conservative field and only a conservative field is equal to zero. A conservative vector field also called a path independent vector field is a vector field f whose line integral c f d s over any curve c depends only on the endpoints of c. The integral is independent of the path that c takes going from its starting point to its ending point.

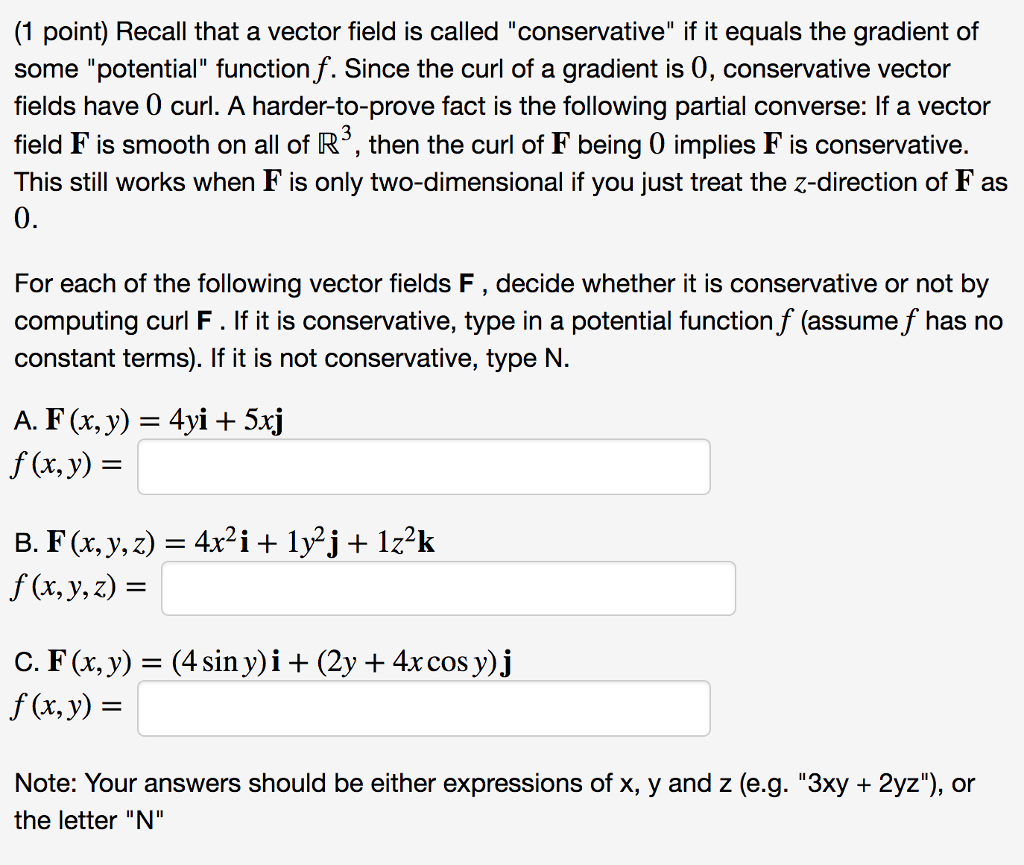
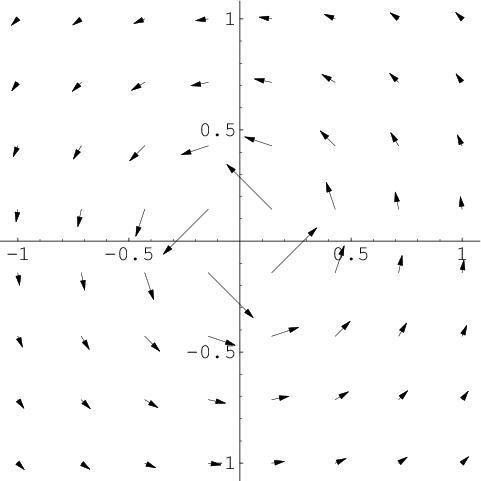
In vector calculus a conservative vector field is a vector field that is the gradient of some function. In three dimensions this means that it has vanishing curl. This in turn means that we can easily evaluate this line integral provided we can find a potential function for f f. If the result equals zerothe vector field is conservative.

Thus we have way to test whether some vector field ar is conservative. If the result is non zerothe vector field is not conservative. A conservative vector field is one which can be written as the gradient of a scalar function. Path independence of the line integral is equivalent to the vector field being conservative.

That is if is a conservative vector field then there is some function such that 1 now the curl of is defined as 2 plugging 1 into 2 we find 3.