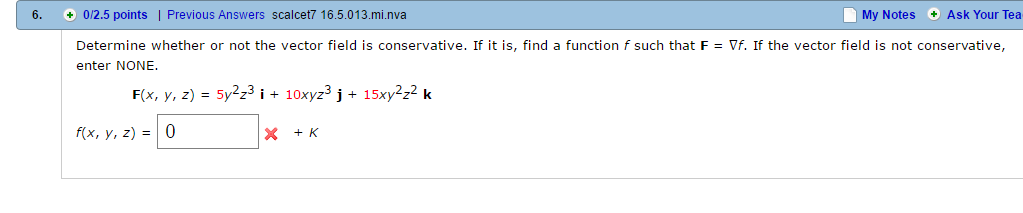
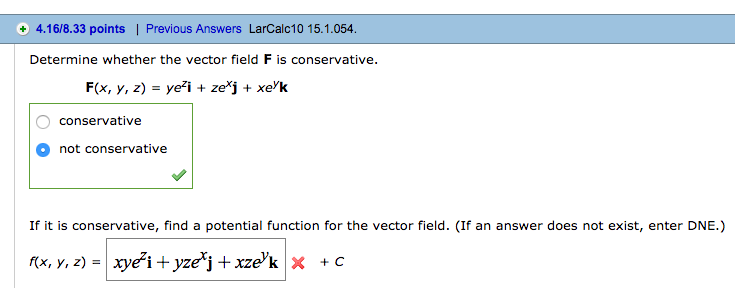
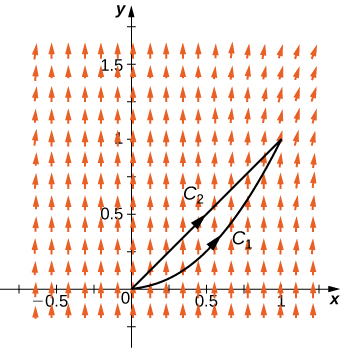
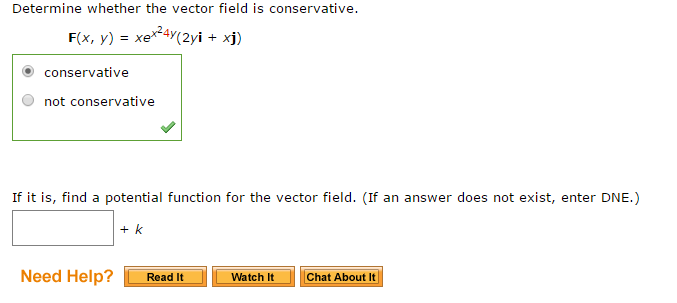
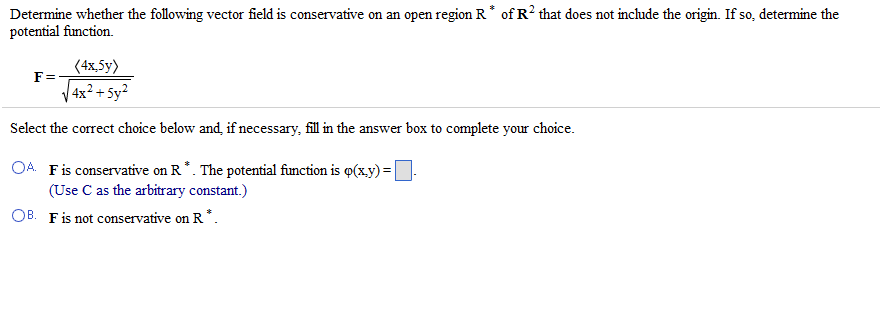
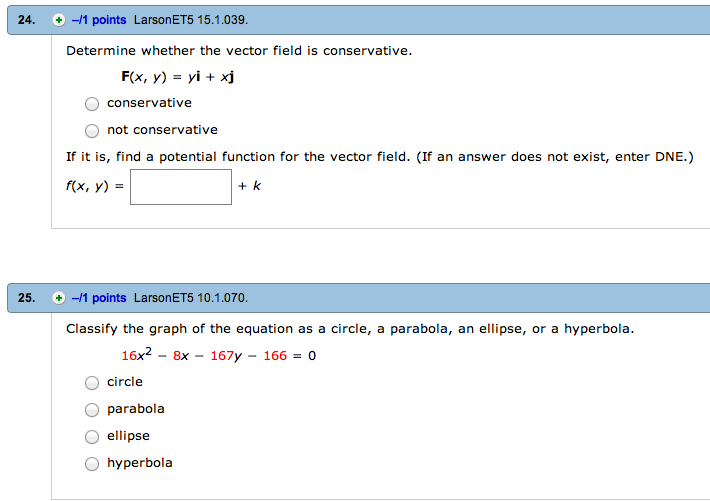
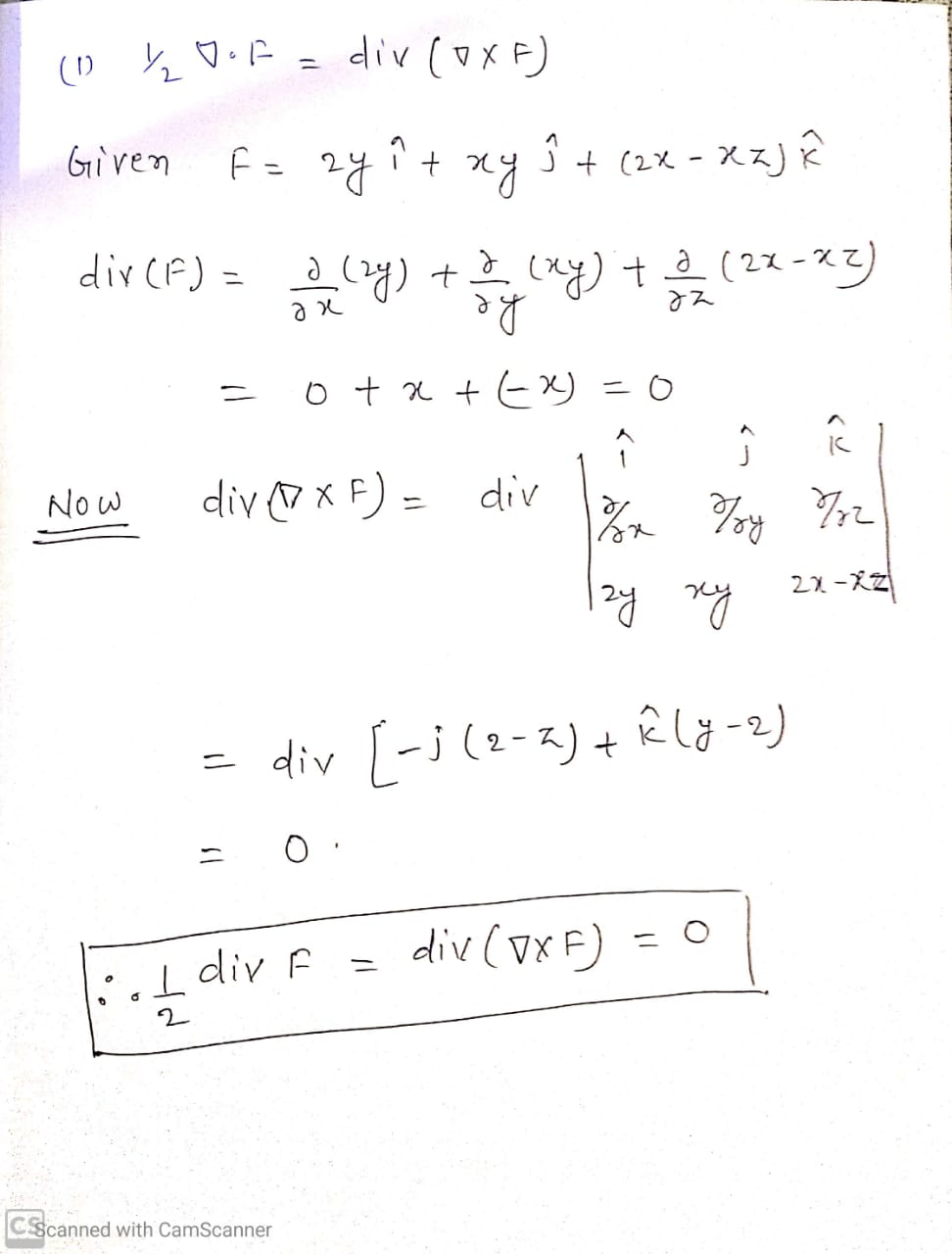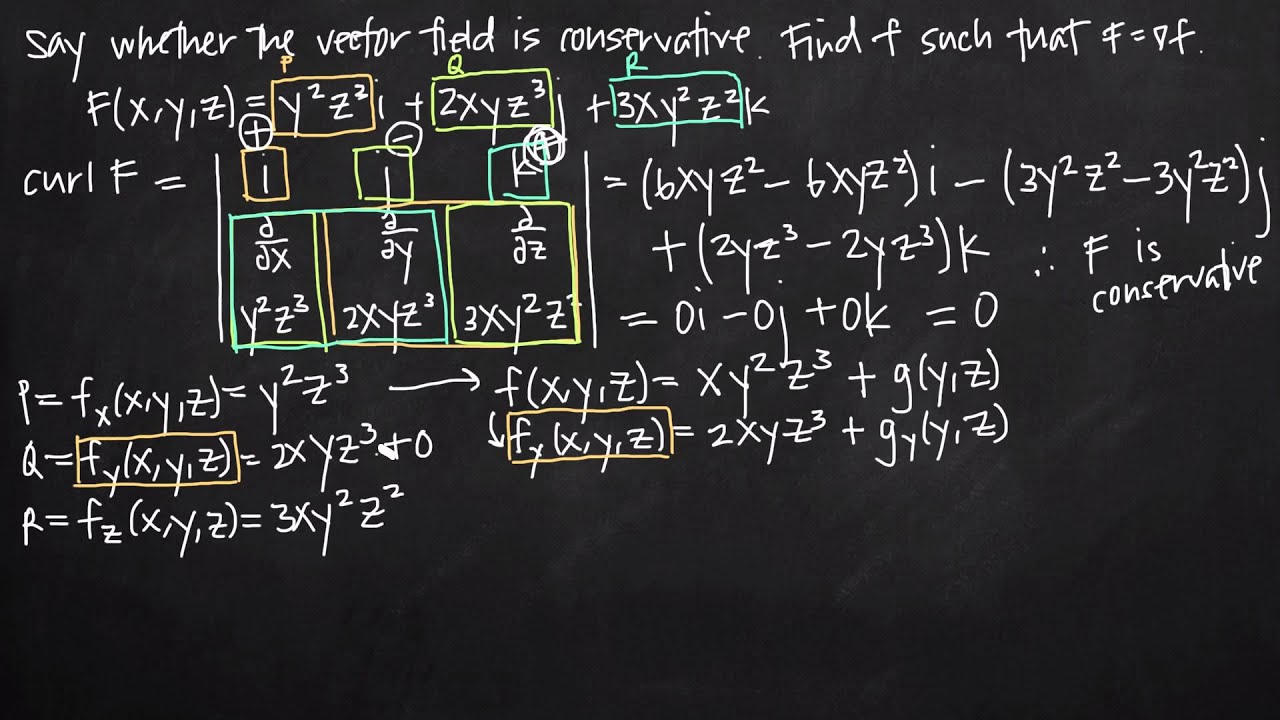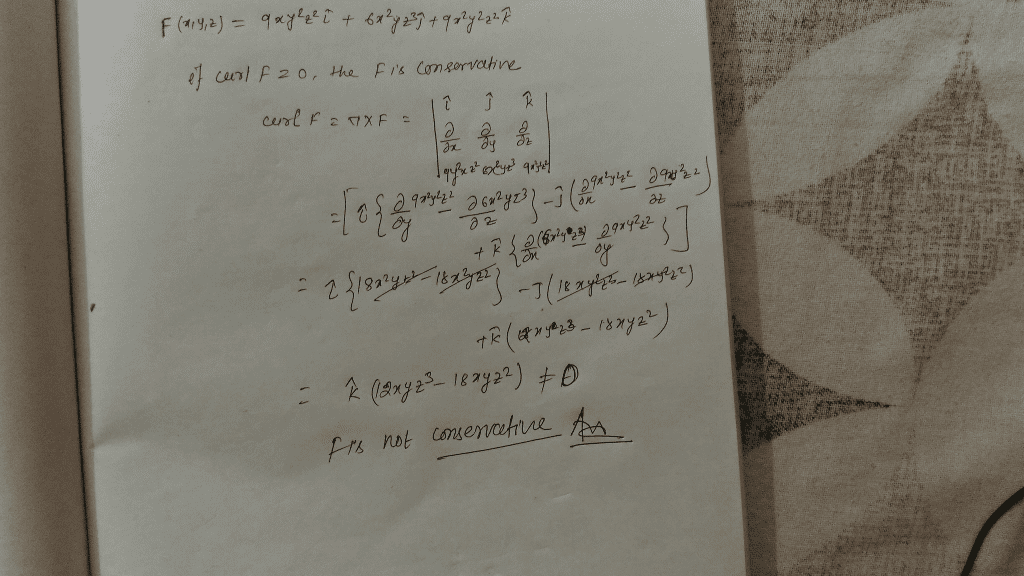Determine Whether The Vector Field Is Conservative Or Not

Fx y z 3y2z3 i 6xyz3 j 9xy2z2 k fx y z k.

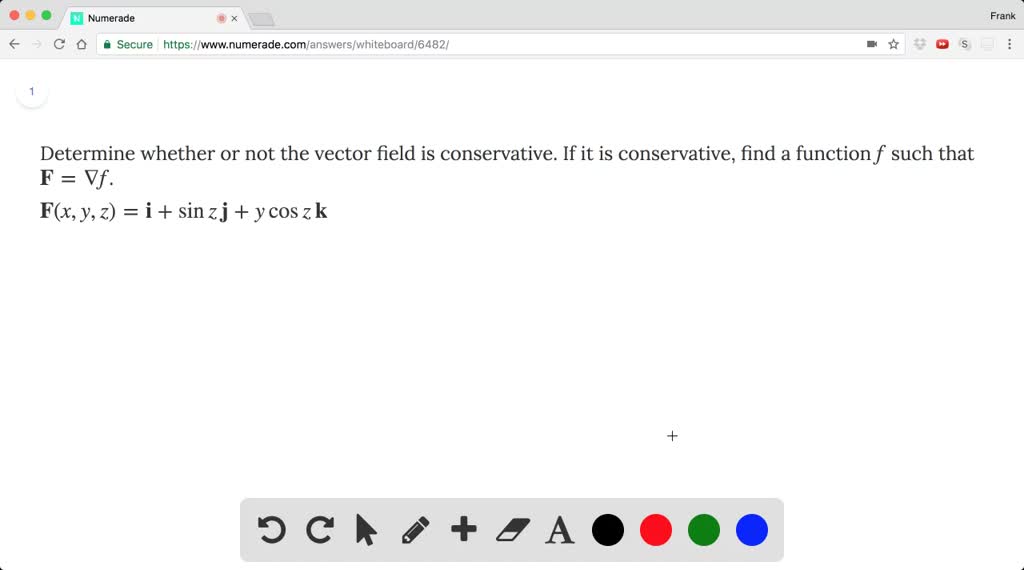
Determine whether the vector field is conservative or not. F x y z i sin z j y cos z k determine whether or not the vector field is conservative. Calculuscalculus mindtap course listdetermine whether or not the vector field is conservative. If it is path independent enter a potential function for it. Determine whether or not the vector field is conservative.

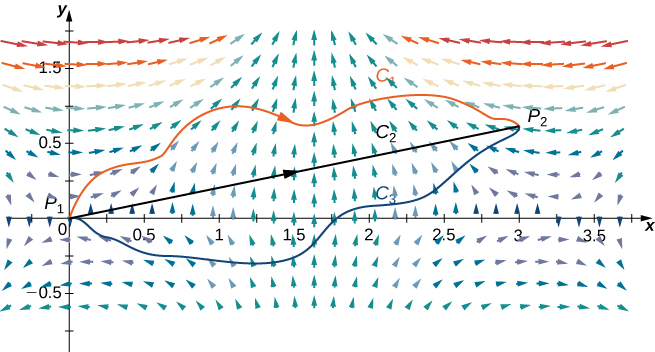
Now given a vector field we want to. Example 1 determine if the following vector fields are conservative or not. F x y z eyzi xzeyzj xyeyzk. Is independent of path.

If it is conservative find a function f such that f v. Lets take a look at a couple of examples. If it is find a function f such that f f. The vector terms inside the integral arise as constants of integration.

Therefore if you are given a potential function f or if you can find one and that potential function is defined everywhere then there is nothing more to do. This is the same force as we started with so the scalar inside the integral is the scalar potential of this vector field. Lets recall that if a vector field is conservative then c. Therefore the curl is zero and f is conservative.

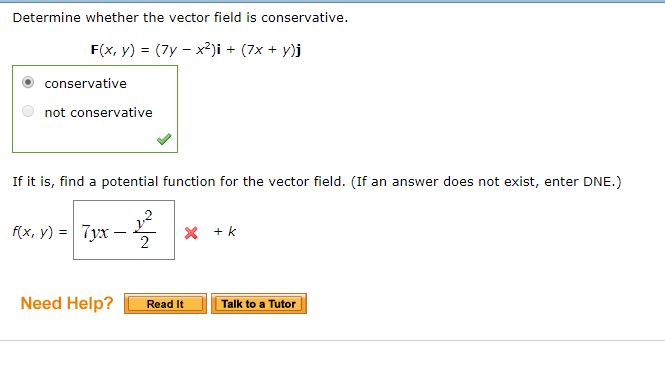
F xy x2yxi y2xyj f x y x 2 y x i y 2 x y j. If it is conservative find a function f such that f f. Determine whether or not the vector field is conservative. They are zero if tz0.

The vector field f defined on r3 which is simply connected. The vector field f f is conservative. This problem has been solved. This comes from that if the vector field is conservative then it is associated to a potential function f such as f and in turn using the fondamental theorem of line integrals.

Determine whether is conservative and. As mentioned in the context of the gradient theorem a vector field f is conservative if and only if it has a potential function f with f f. Determine whether or not the vector field is conservative. If it is conservative find a function f such that.

If the vector field is not conservative enter dne fx y 2 10xi 5x 18y2j 9yk fx y z. If it is path dependent enter. We can show path independence if the curl is zero. Determine whether each of the following vector fields f is path independent conservative or not.