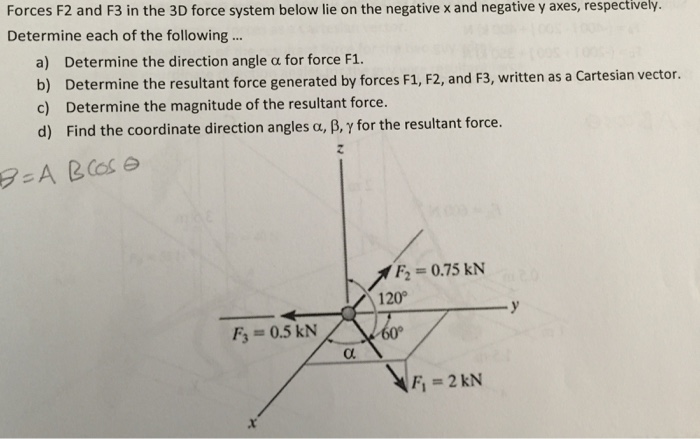
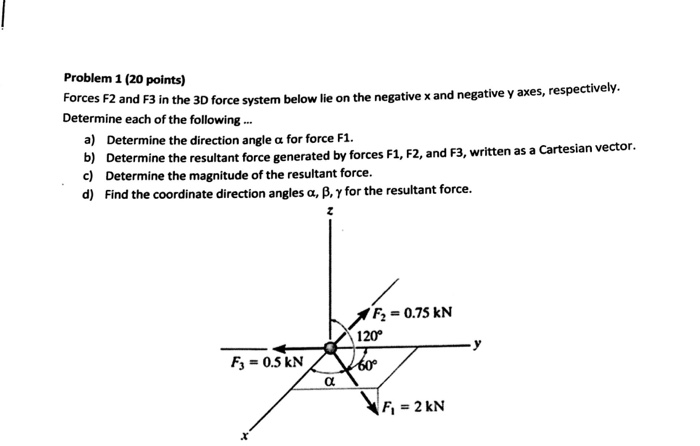
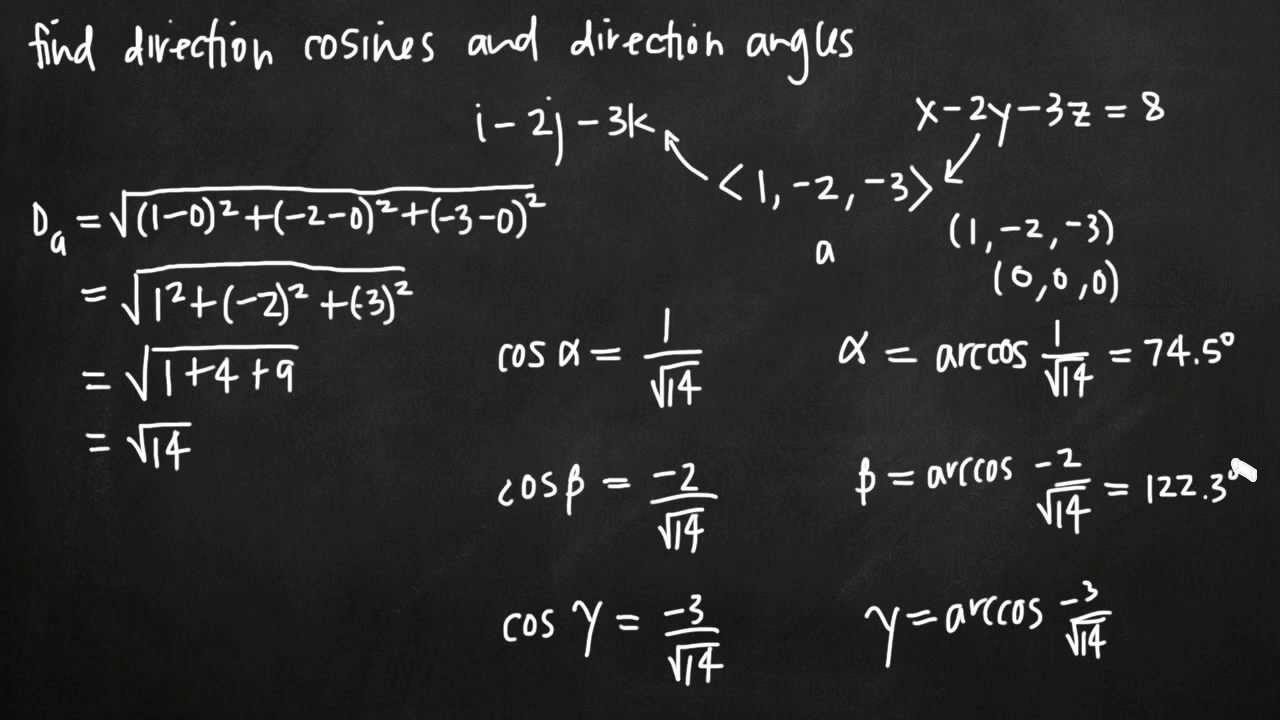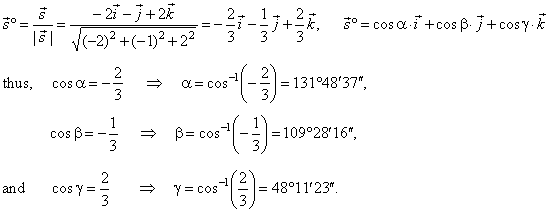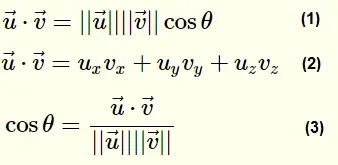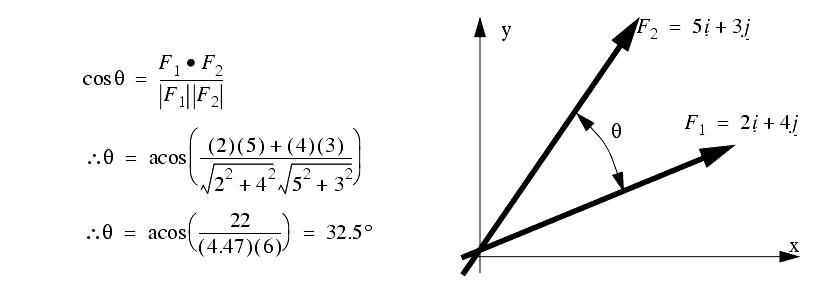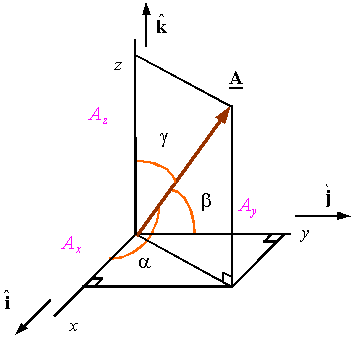Direction Angle Of A Vector 3d

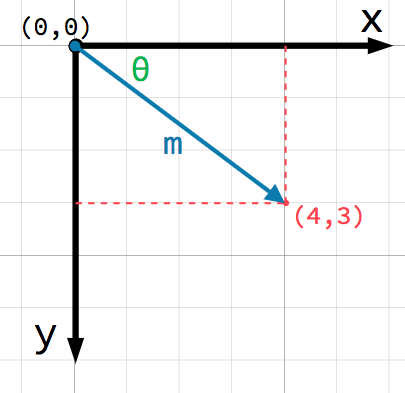
If you subtract 180 degrees from your answer of 45 degrees you get 135 degrees which is your actual angle measured from the positive x axis in the clockwise direction.

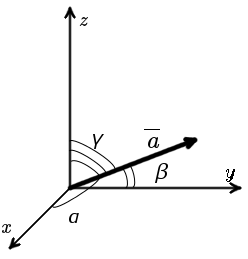
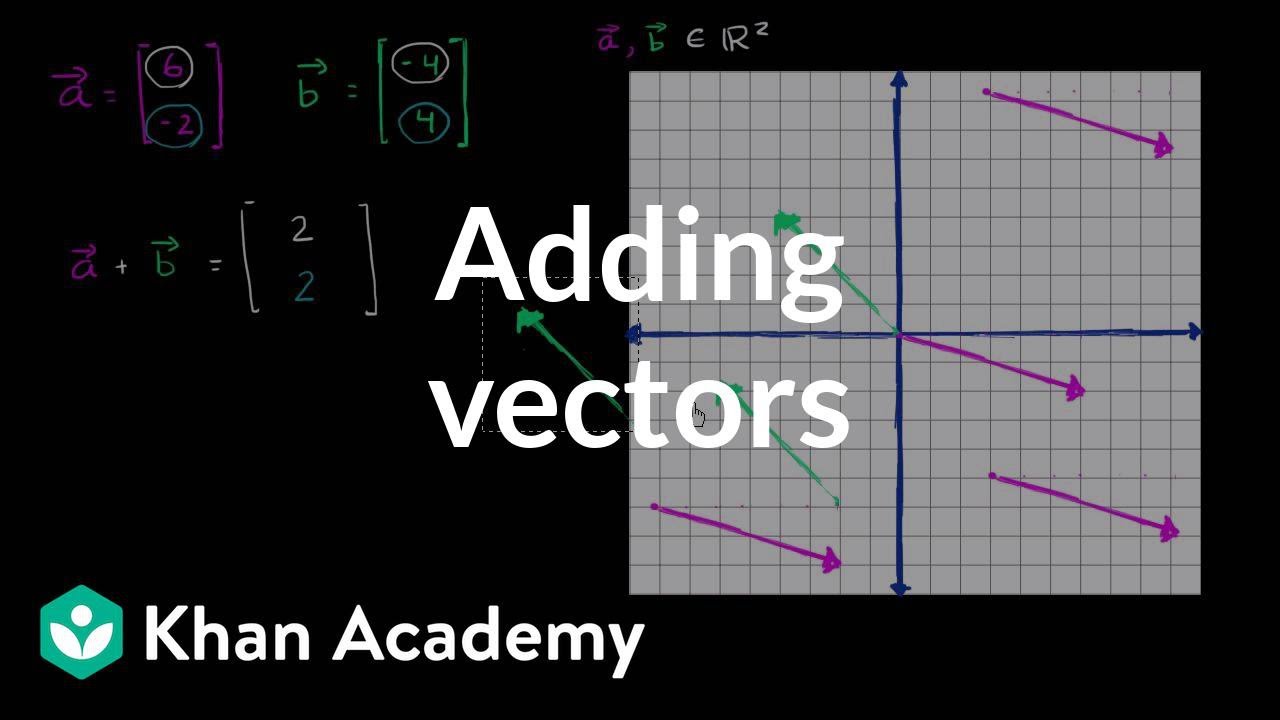
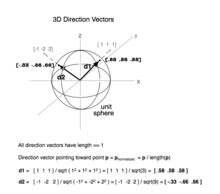
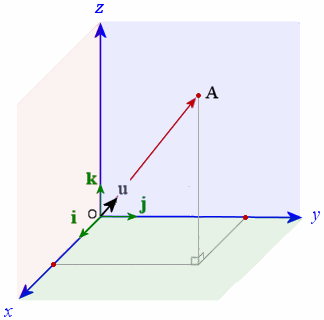
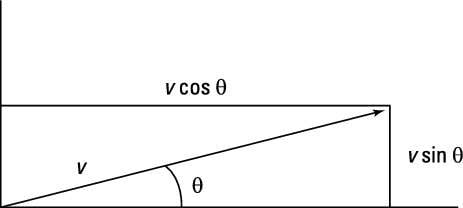
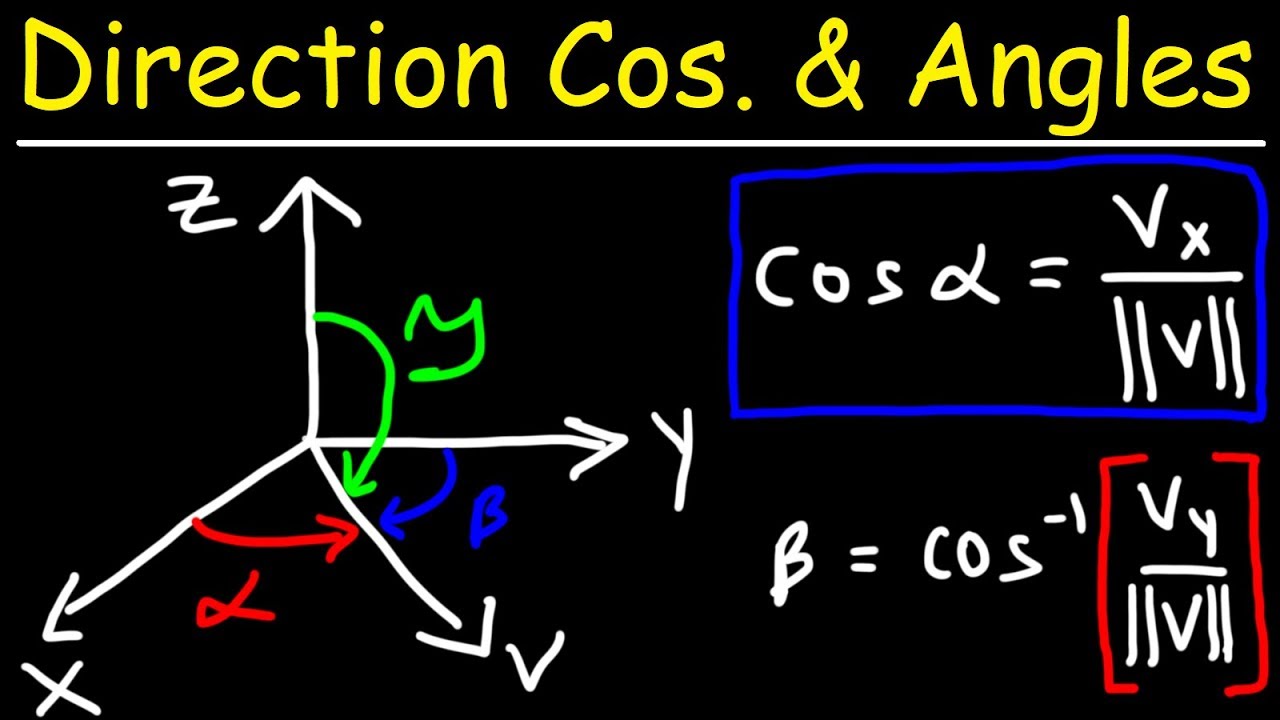
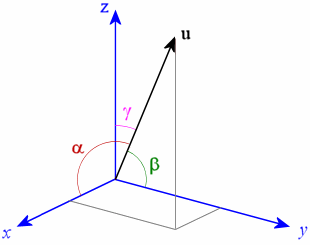
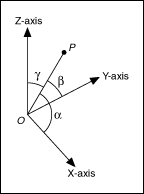
Direction angle of a vector 3d. This calculus 3 video tutorial explains how to find the direction cosines of a vector as well as the direction angles of a vector. The direction as seen when you look at the y z plane will be arctan 06511 3058 degrees. U x y coso sino cosoi sino j any vector that makes an angle o with the positive x axis can be written as the unit vector times the magnitude of the vector. Suppose also that we have a unit vector in the same direction as oa.

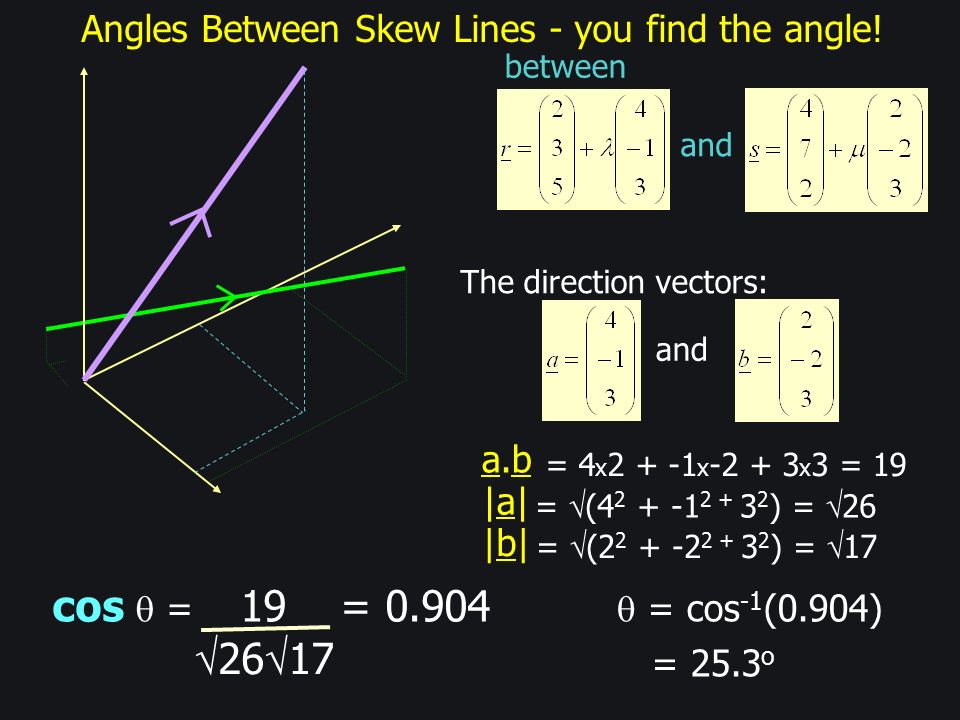
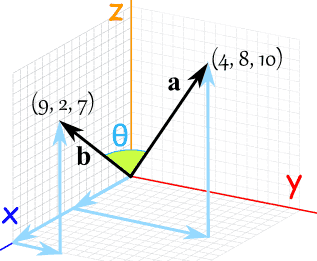
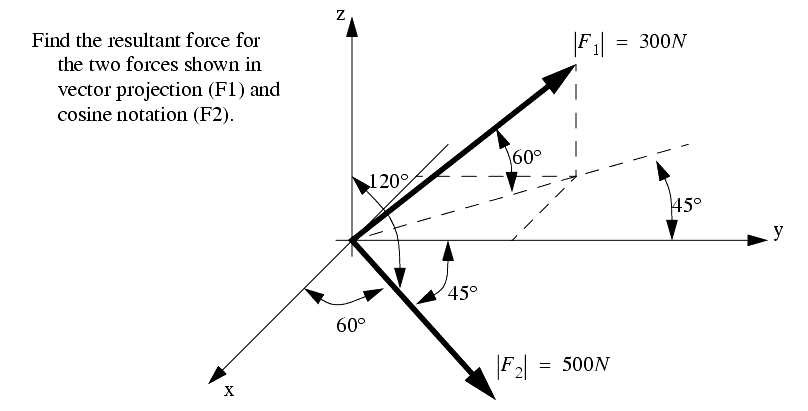
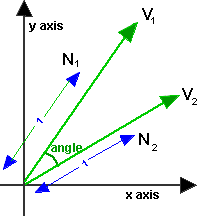
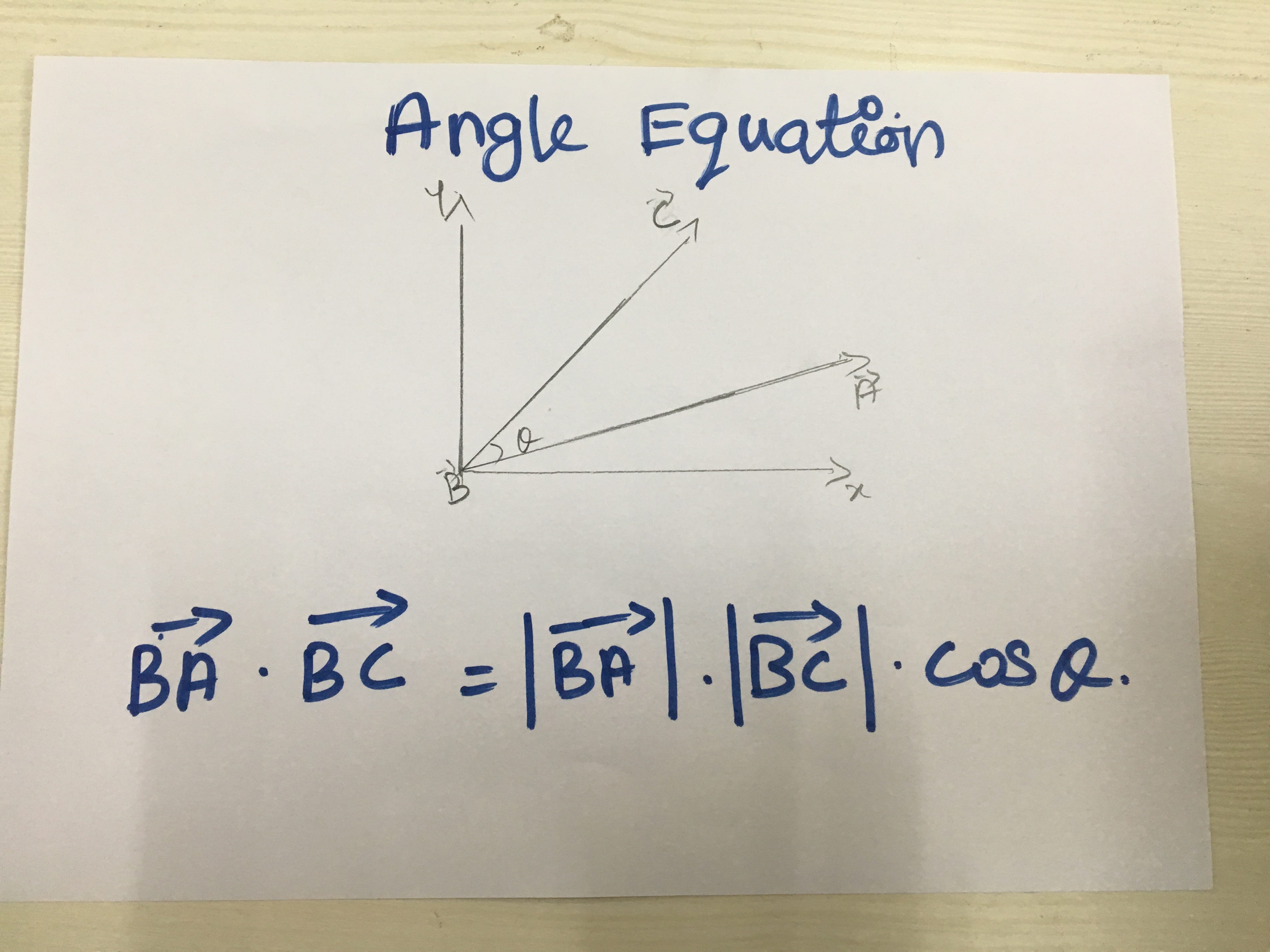
Below are given the definition of the dot product 1 the dot product in terms of the components 2 and the angle between the vectors 3 which will be used below to solve questions related to finding angles between two vectors. Let our unit vector be. This is the angle that the projection of your vector in the x y plane makes with the x axis. Angle between two 3d vectors.

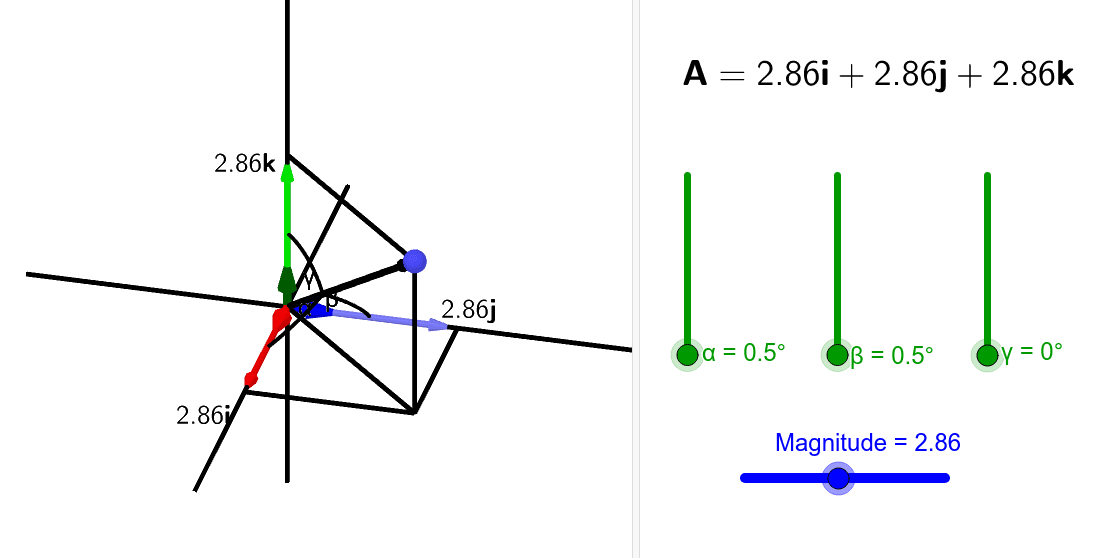
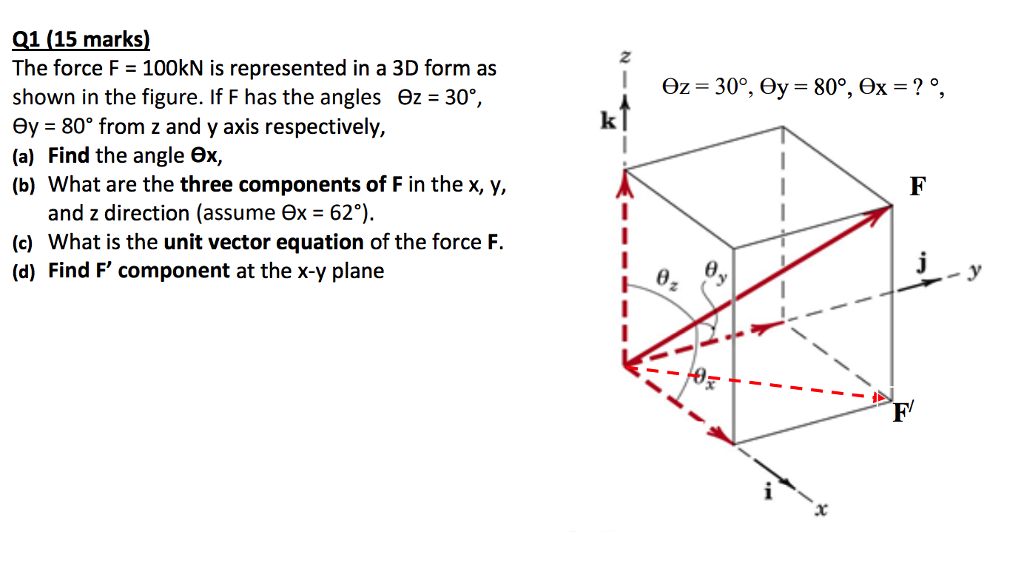
Alternatively you could reason that since the components of the vector are both negative you must be between 180 degrees and 270 degrees. The 3d vectors are using the x y z axes. A is the angle between u and the x axis. Calculate the angle of three dimensional vectors 3d vectors with entered vector coordinates.

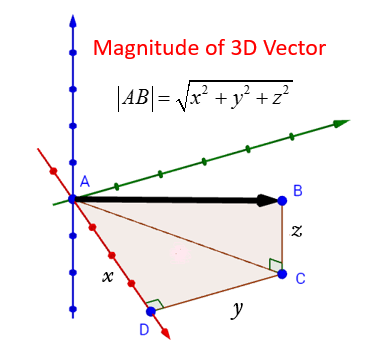
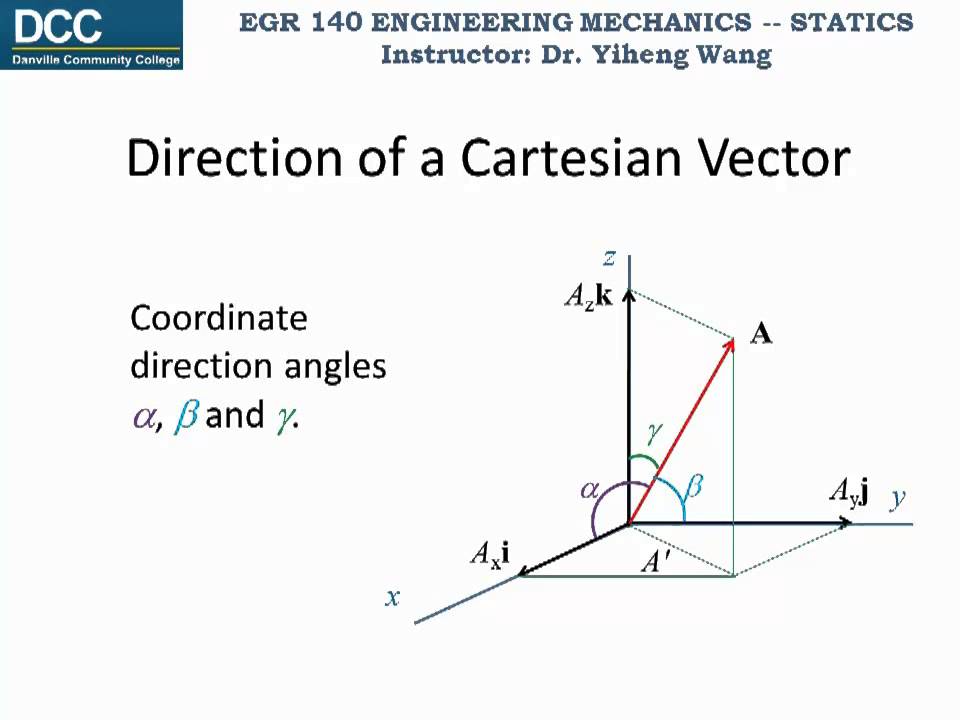
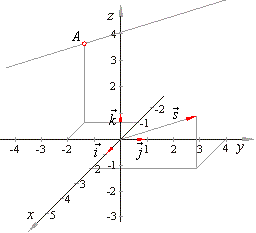
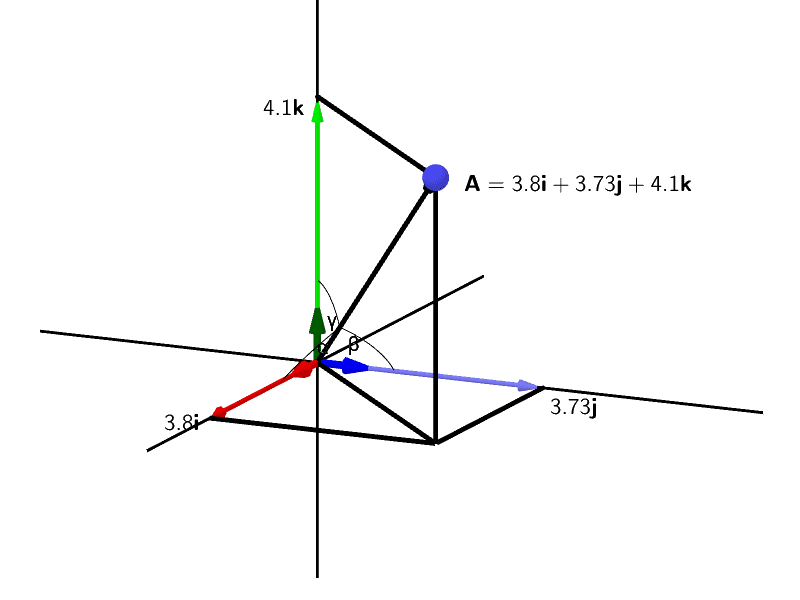
Similarly a vector a in the right diagram which is directed from a point p 1 x 1 y 1 z 1 to a point p 2 x 2 y 2 z 2 in space equals to sum of its vector components a x i a y j and a z k in the direction of the coordinate axes x y and z respectively that is. Step by step solution. The angle o is called the directional angle of vector u. U u 1 i u 2 j u 3 k.

The terminal point of vector u lies on a unit circle and thus u can be denoted by. Go here for a reminder on unit vectors.