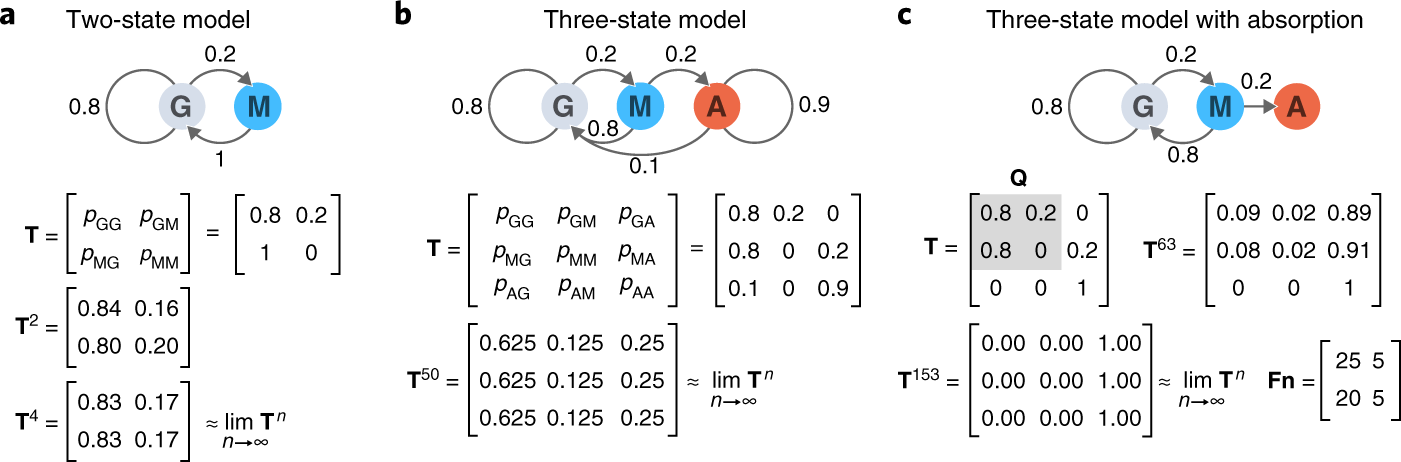
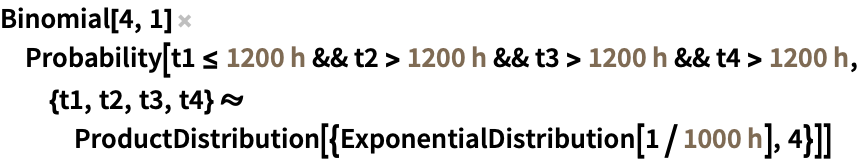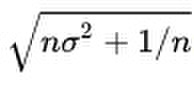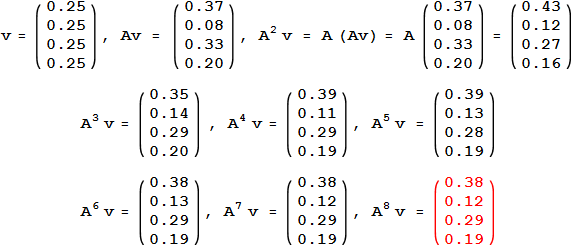Fixed Probability Vector Definition

Find the probability of remaining in state 2 in two observations.

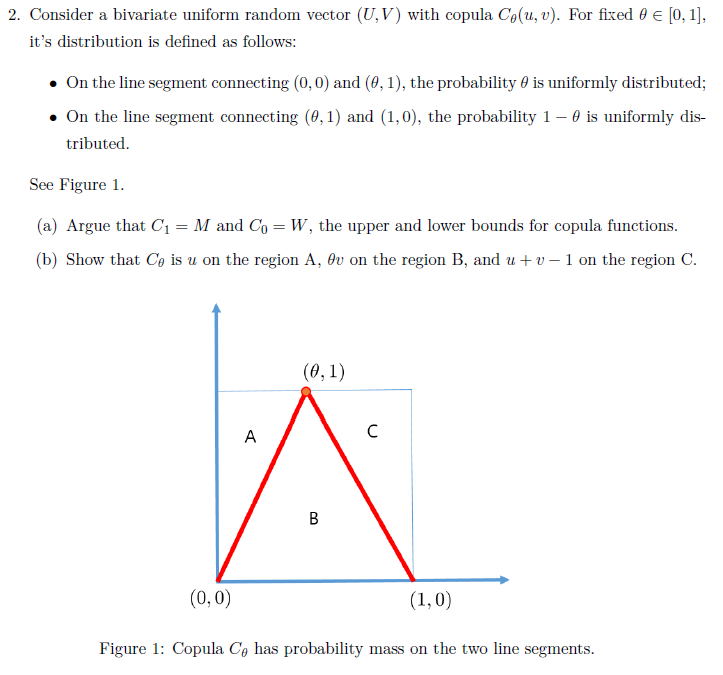
Fixed probability vector definition. Consider the markov chain on s 01234 which moves a step to the right with probability 12 and to the left with probability 12 when it starts at 123. When dealing with multiple random variables it is sometimes useful to use vector and matrix notations. If it is at 0 then assume it moves to 1 with probability 1 and if it as at 4 it moves to 3. Find the fixed probability vector t.

A probability vector is a vector in which all the entries are non negative and add up to exactly one. Vector is an object which has magnitude and direction both. A markov chain is a sequence of probability vectors x 0x 1x 2 together with a stochastic matrix p such that x 1 px 0x 2 px 1x 3 px 2 a markov chain of vectors in rn describes a system or a sequence of experiments. Find the xed stationary probability vector for p 34 14 0 0 23 13 14 14 12.

This makes the formulas more compact and lets us use facts from linear algebra. An example is the crunch and munch breakfast problem. An n dimensional probability vector may represent the probability distribution of a set of n variables. X k is called state vector.

The nxn matrix whose ij th element is is termed the transition matrix of the markov chain. Find the probability of remaining in state 1 in one observation. Its sometimes also called a stochastic vector. It is easily seen that the stationary probability corresponds to the probabilities of the states being taken from the eigenvector of the transition matrix their value does not change by running the markov model.

If a system featuring n distinct states undergoes state changes which are strictly markov in nature then the probability that its current state is given that its previous state was is the transition probability. In mathematics and statistics a probability vector or stochastic vector is a vector with non negative entries that add up to one. The positions indices of a probability vector represent the possible outcomes of a discrete random variable and the vector gives us the probability mass function of that random variable which is the standard way of characterizing a discrete probability distribution. Whereas moduli of vector components squared for a given vector give a fixed probability distribution moduli of matrix elements squared are interpreted as transition probabilities just as in a random process.