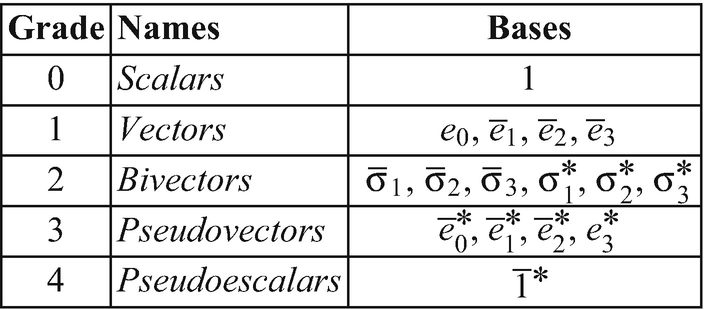
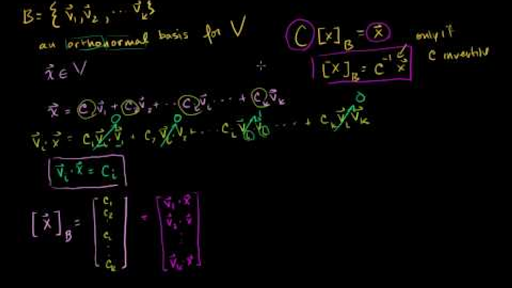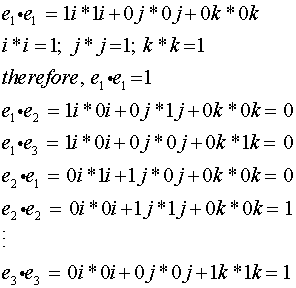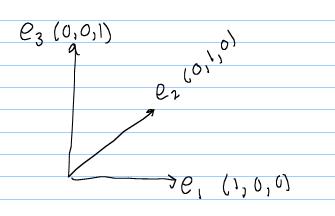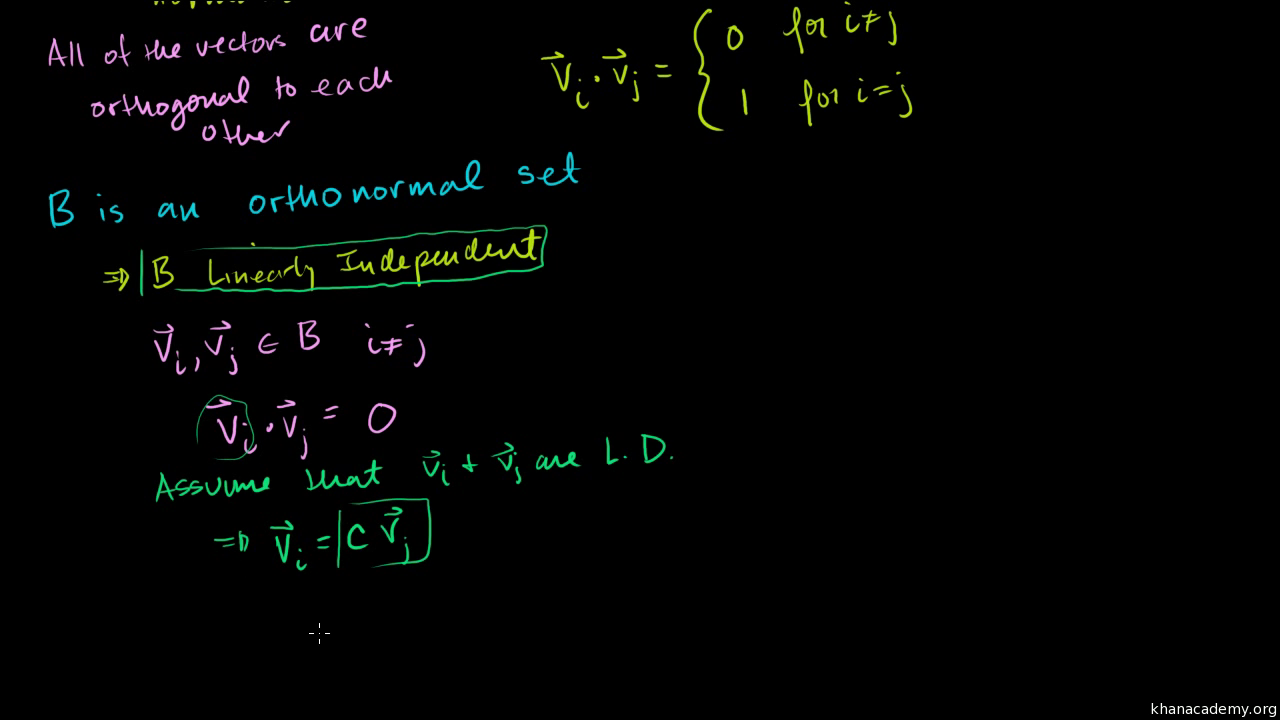Given Two Vectors Expressed In The Same Common Orthonormal Basis E1 E2 E3

So if we wanted to find an orthonormal basis for the span of v1 let me write this down. This is just a basis. In mathematics particularly linear algebra an orthonormal basis for an inner product space v with finite dimension is a basis for v whose vectors are orthonormal that is they are all unit vectors and orthogonal to each other.
given two vectors expressed in the same common orthonormal basis e1 e2 e3

Orthonormal bases in hilbert space.

Given two vectors expressed in the same common orthonormal basis e1 e2 e3. We will represent vectors in a cartesian basis where the basis vectors e i are orthonormal ie. Lets say i have a orthonormal set of vectors v1 v2. R2to r3 determine the dimension of a mysterious vector space from coordinate vectors. Find an orthonormal basis of the given two dimensional vector space the current problem.

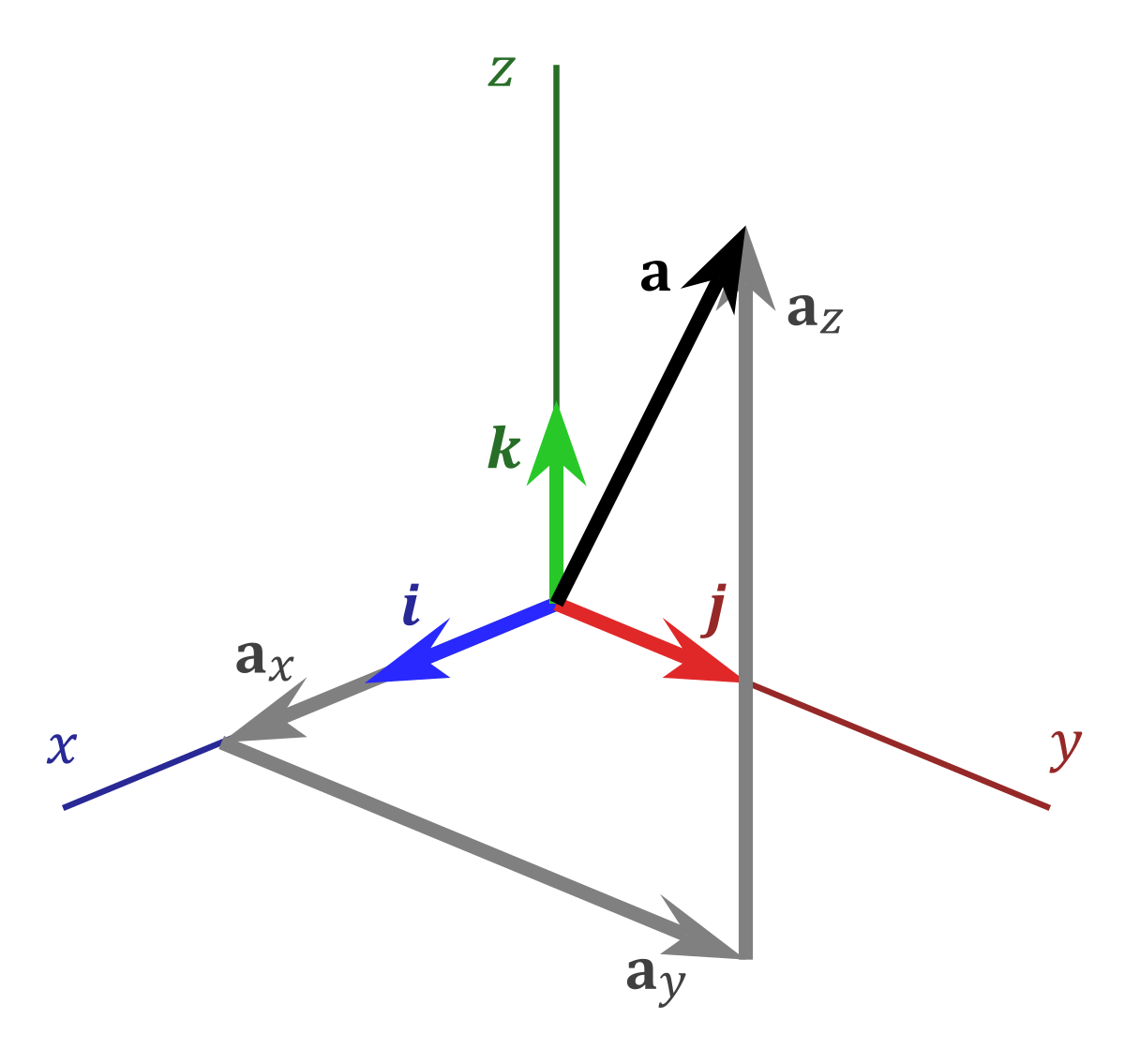
Find a basis of the subspace spanned by four polynomials of degree 3 or less. In the index notation the expression for the vector a in terms of the components a1 a 2 a3 and the corresponding basis vectors e1 e 2 e 3 is written as 3 a a1e1 a 2 e 2 a3 e 3 ai e i 138 i 1. They have unit length and they are orthogonal with respect to each other. 2 4 1 0 2 0 3 5 2 4 0 3 5 using the component extraction rule for tensors nd t 12 and t 33 in the e a basis.

E1 e2 e3 e3 e1 e2 p6 rad 9. Lets find an orthonormal basis. 1 axioms of addition. Answer to problem given two vectors expressed in the same common orthonormal basis e1e2 e3.

Assume e i and e a are as de ned in problem 8. Ririei 7363 r2 r2d2 2rie3 w. Tensor component extraction consider a 2nd order tensor twhose components in the e i basis are given by t. V1left frac12 stack exchange network stack exchange network consists of 177 qa communities including stack overflow the largest most trusted online community for developers to learn share their knowledge and build their careers.

This can be expressed using dot products e 1 e 1 1 e 2 e 2 1 e 2 e 3 1 e 1 e 2 0 e 1 e 3 0 e 2 e 3 0. Lets call this vector up here lets call that v1 and lets call this vector right here v2. For example the standard basis for a euclidean space r n is an orthonormal basis where the relevant inner product is the dot product of vectors. 1a set of vectors v 1.

Can be represented as a linear combination of basis vectors. Determine whether each set is a basis for r3 express the eigenvalues of a. Denition 01 a linear space is a nonempty set l together with a mapping from l l into l called addition denoted xy 7x y and a mapping from the cartesian product of either r or c with l into l called scalar multiplication denoted x 7x which satisfy the following properties. These guys right here are just a basis for v.

Do not try and assemble the rotation tensor.