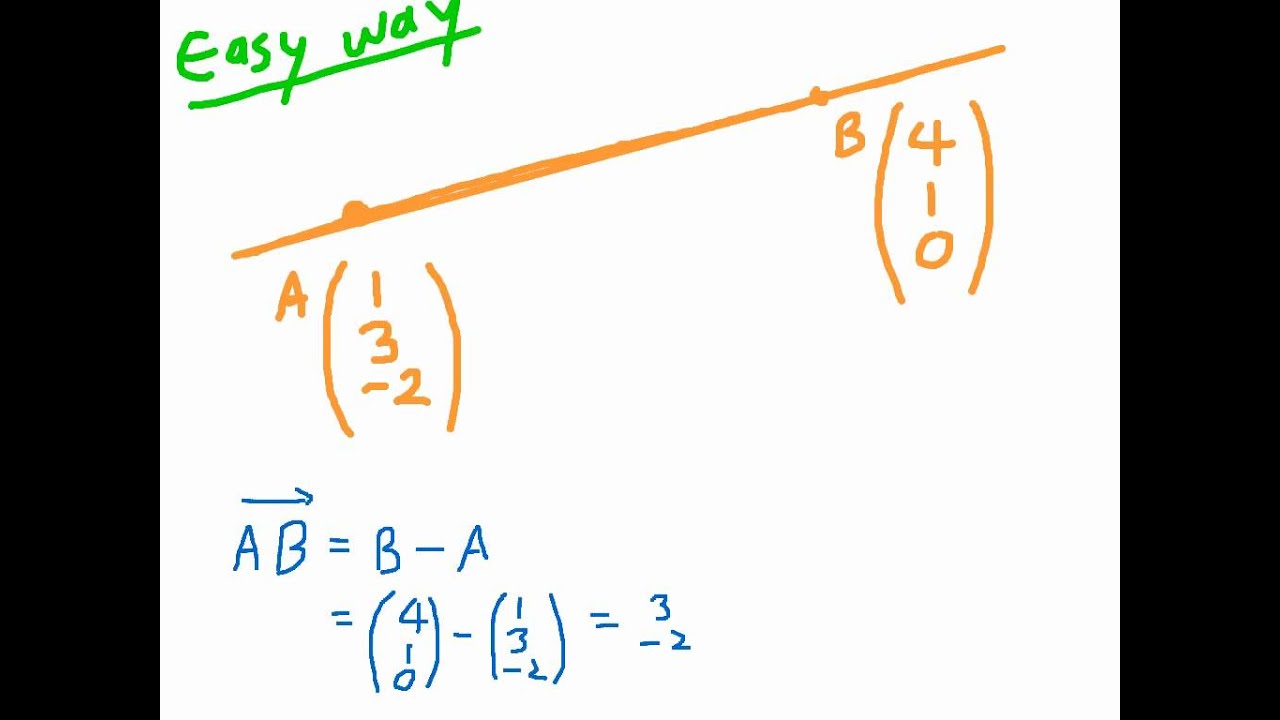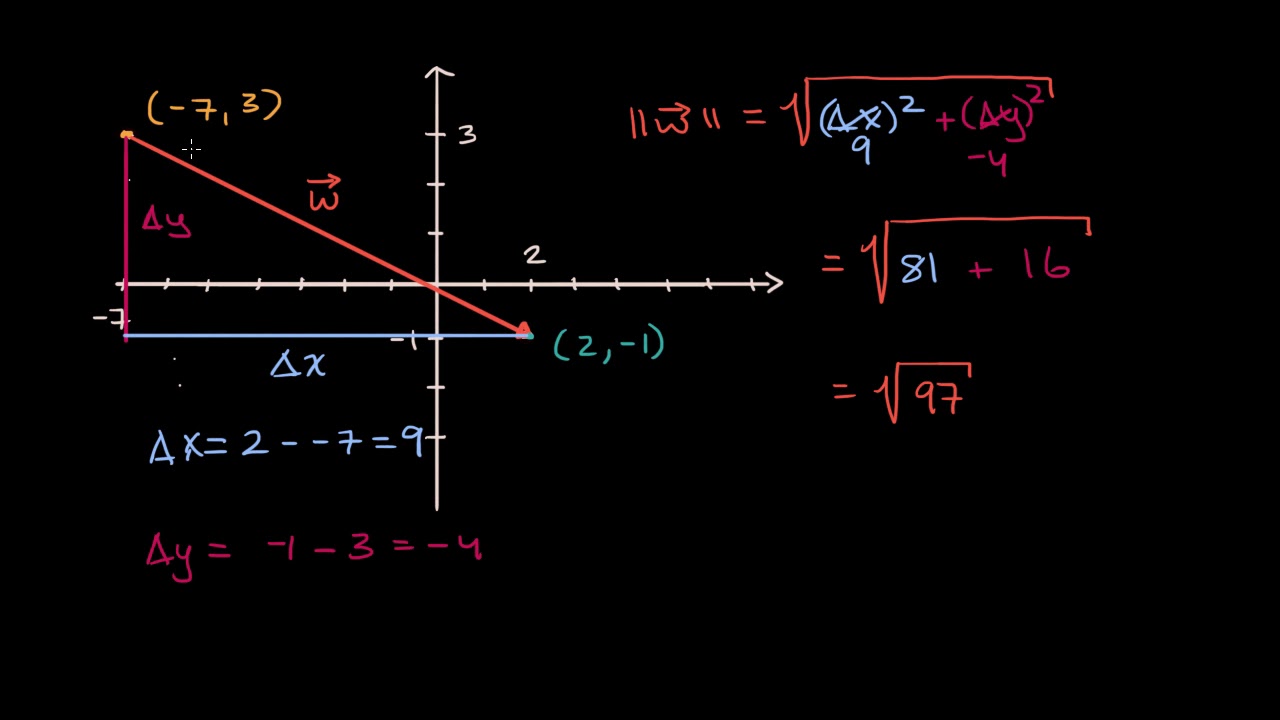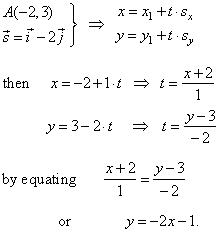How To Find The Vector Equation Of A Line Given 2 Points

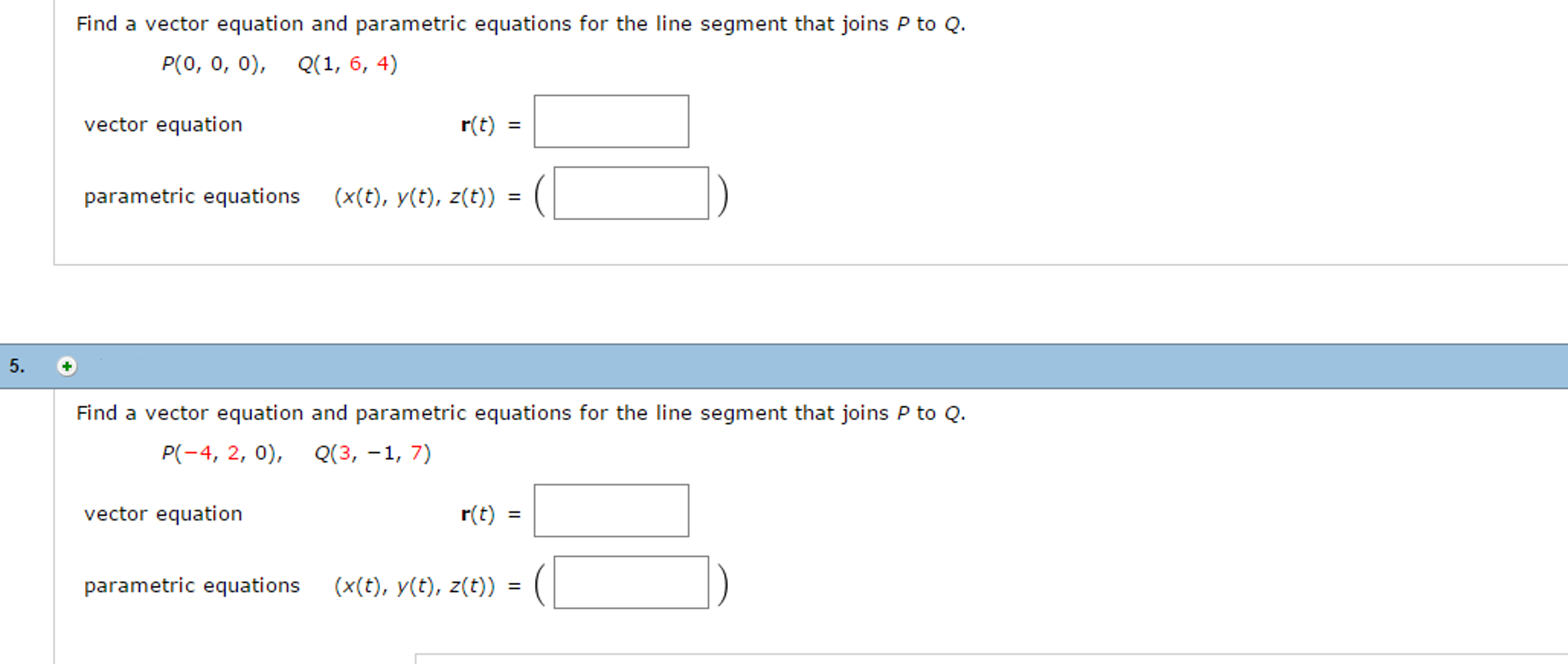
To find the parametric equations of the line passing through the point 123 and parallel to the vector 30 1 we first find the vector equation of the line.

How to find the vector equation of a line given 2 points. Here r0 123 and v30 1. Note that a line is continuous and defined on the real line. Second calculator finds the line equation in parametric form that is. The point 125 is 12 units along and 5 units up steps.

Determining a vector given two points fold unfold. This was requested via twitter atmathormaths. In order to find the direction vector we need to understand addition and scalar multiplication of vectors and the vector equation of a line can be used with the concept of parametric equations. It also outputs direction vector and displays line.

These online calculators find the equation of a line from 2 points. Vectors with initial points not at the origin. It is important to note that the equation of a line in three dimensions is not unique. A line is comprised of a position and a direction so youre going to have two vectors.

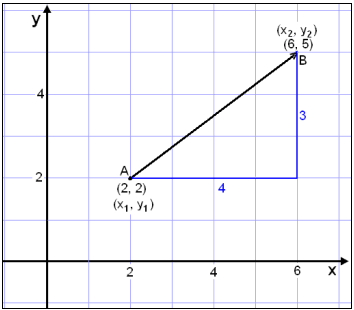
First we find the the direction vector by subtracting the two points. There are 3 steps to find the equation of the straight line. Find the slope of the line. A tutorial on how to find a vector from one point to another and hence find the vector equation of a straight line through two points.

We use cartesian coordinates to mark a point on a graph by how far along and how far up it is. Might as well use one of the two you listed. Choosing a different point and a multiple of the vector will yield a different. Thus the line has vector equation r 123t30 1.

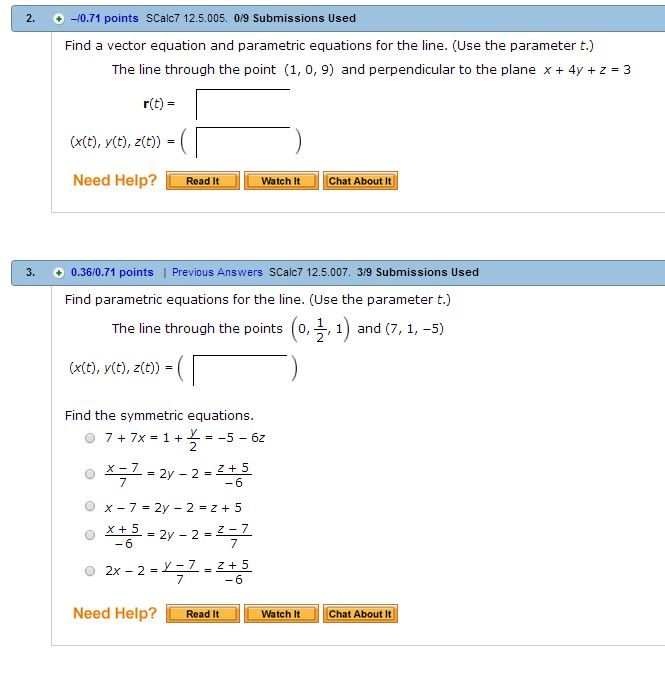
The end result should be of the from p p0 td. It also outputs slope and intercept parameters and displays line on a graph. The vector equation of the line through two points is the sum of one of the points and the direction vector between the two points scaled by a variable. In order to create the vector equation of a line we use the position vector of a point on the line and the direction vector of the line.

T is the position along the line in increments the length of d which is usually normalized to 1 po position can be any point on the line. First calculator finds the line equation in slope intercept form that is. P0 4 5 0. Put the slope and one point into the point slope formula 3.

Remember that a vector consists of both an initial point and a terminal point.