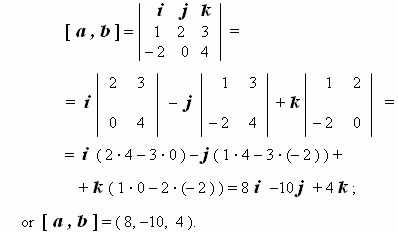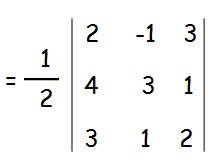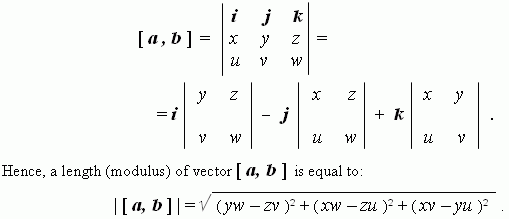How To Prove Vectors Are Collinear

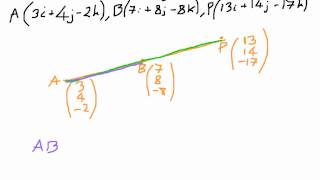
Let a 2 1 3 b 4 3 1 and c 3 1 2 are collinear.

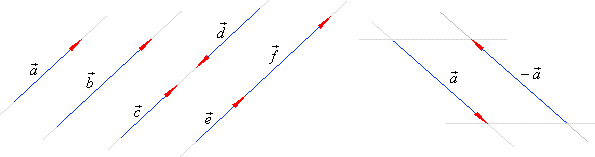
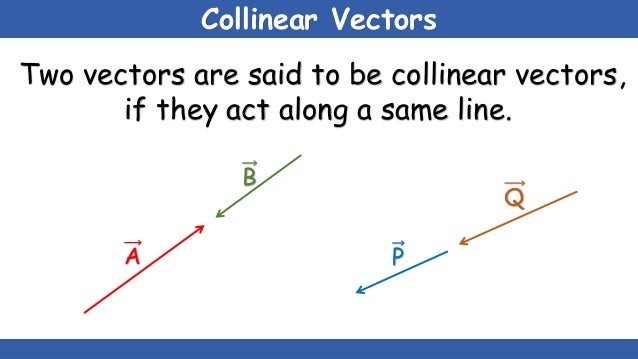
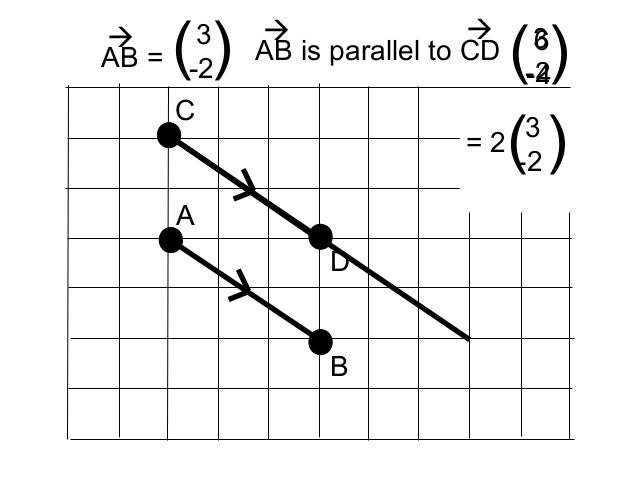
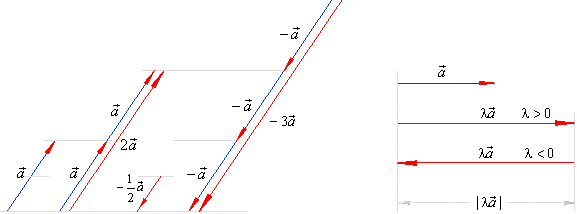
How to prove vectors are collinear. Oabc is a parallelogram. When youre working in three dimensions the only way to prove that three points are in a line collinear involves showing that a common direction exists. In other words to prove collinearity we would need to show ab kac a b k a c for some constant k k. Two vectors are collinear if their cross product is equal to the zero vector.

Two vectors are collinear if relations of their coordinates are equal. Show that the points 2 1 3 4 3 1 and 3 1 2 are collinear. Three or more points that lie on a same straight line are called collinear points. How to prove points are collinear using vectors.

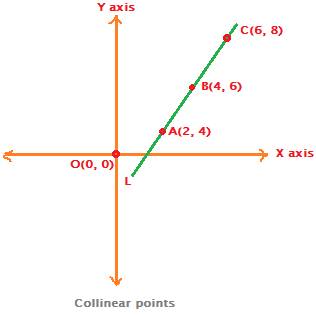
One way is by using determinant the other way is let abc be there points using coordinates make two vector a vectorab and b vector bc. Condition of vectors collinearity 3. Is represented by the vector and is represented by the vector. Consider a straight line l in the above cartesian coordinate plane formed by x axis and y axis.

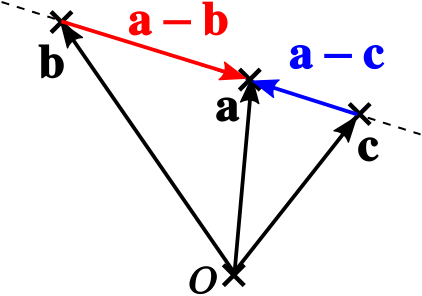
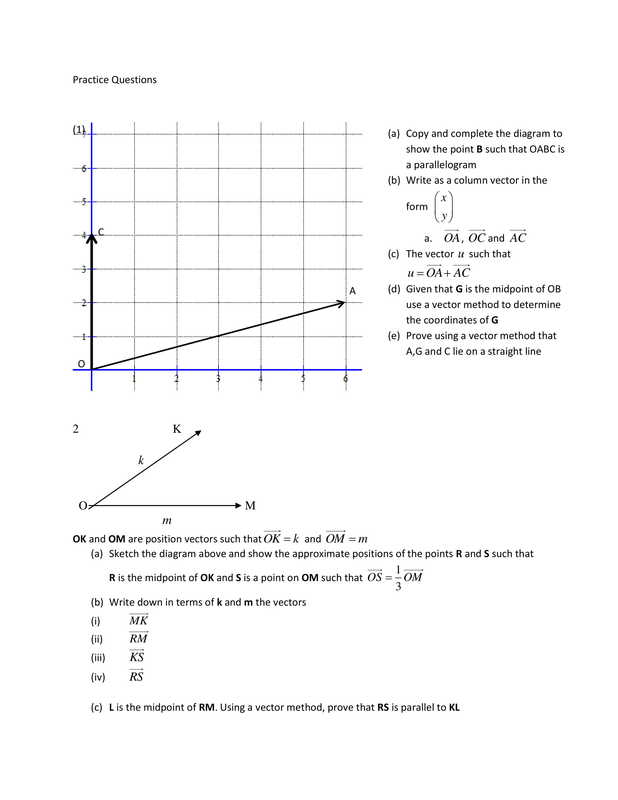
M is the mid point of bc and n is the point on ob such that onnb 21. Three points with position vectors a a b b and c c are collinear if and only if the vectors ab a b and ac a c are parallel. For this you need to use vectors. Here we are going to see how to prove points are collinear using vectors.

Condition 2 is not valid if one of the components of the vector is zero. This straight line l is passing through three points a b and c whose coordinates are 2 4 4 6 and 6 8 respectively.