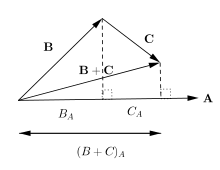
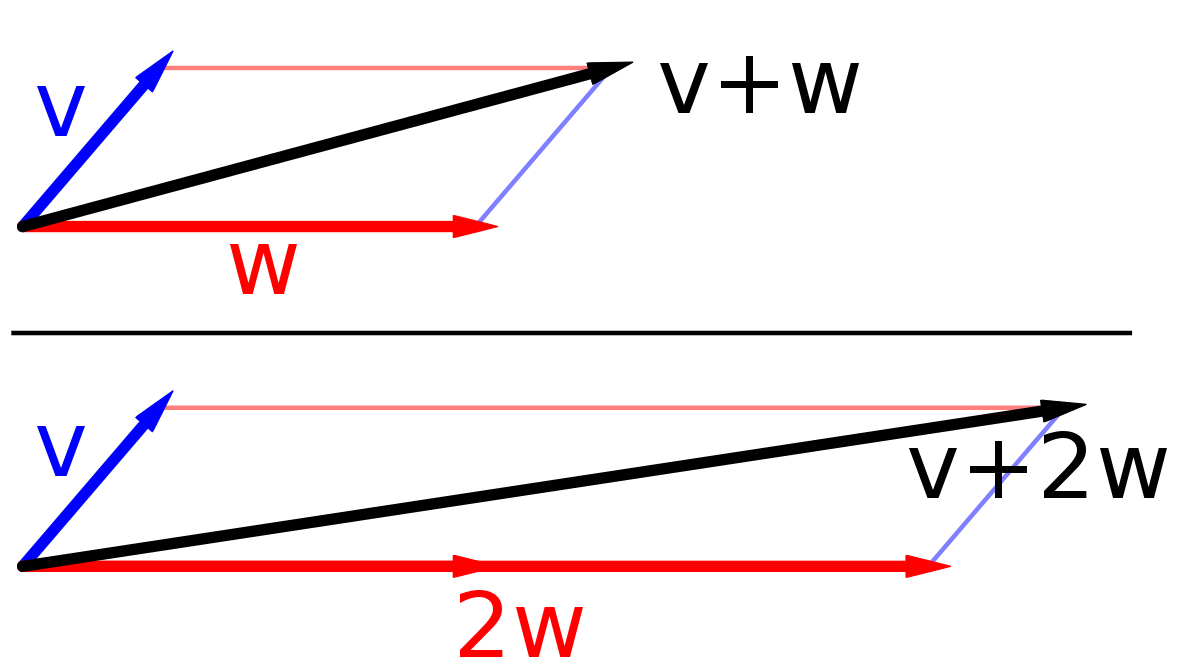
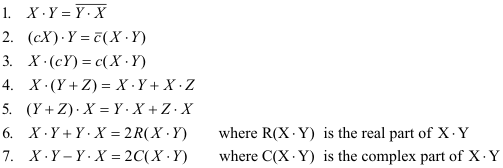Inner Product Complex Vector Space

2 to say that h is a complex inner product space means that h is a complex vector space on which there is an inner product x y associating a complex number to each pair of.

Inner product complex vector space. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors. In linear algebra an inner product space is a vector space with an additional structure called an inner product. Introduced by dirac called bra ket notation. Inner products allow the rigorous introduction of intuitive geometrical notions such as the length of a vector or the angle between two vectors.

Although we are mainly interested in complex vector spaces we begin with the more familiar case of the usual inner product. Inner product spaces isaiah lankham bruno nachtergaele anne schilling march 2 2007 the abstract denition of vector spaces only takes into account algebraic properties for the addition and scalar multiplication of vectors. Huvwi huwihvwi and huv wi huvihuwi. Inner product spaces generalize e.

Section 27 inner products for complex vectors. Column matrices play a special role in physics where they are interpreted as vectors or in quantum mechanics statesto remind us of this uniqueness they have their own special notation. They also provide the means of defining orthogonality between vectors. 1 real inner products let v v.

When we say that a vector space v is an inner product space we are also thinking that an inner product on vis lurking nearby or is obvious from the context or is the euclidean inner product if the vector space is fn. In bra ket notation a column matrix called a ket can be written. A hilbert space h is a real or complex inner product space that is also a complete metric space with respect to the distance function induced by the inner product. A complex vector space with a complex inner product is called a complex inner product space or unitary space.

Denition a hermitian inner product on a complex vector space v is a function that to each pair of vectors u and v in v associates a complex number huvi and satises the following axioms for all u v w in v and all scalars c. Show that the func tion defined by is a complex inner product. An inner product space is a vector space along with an inner product on that vector space.