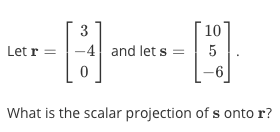
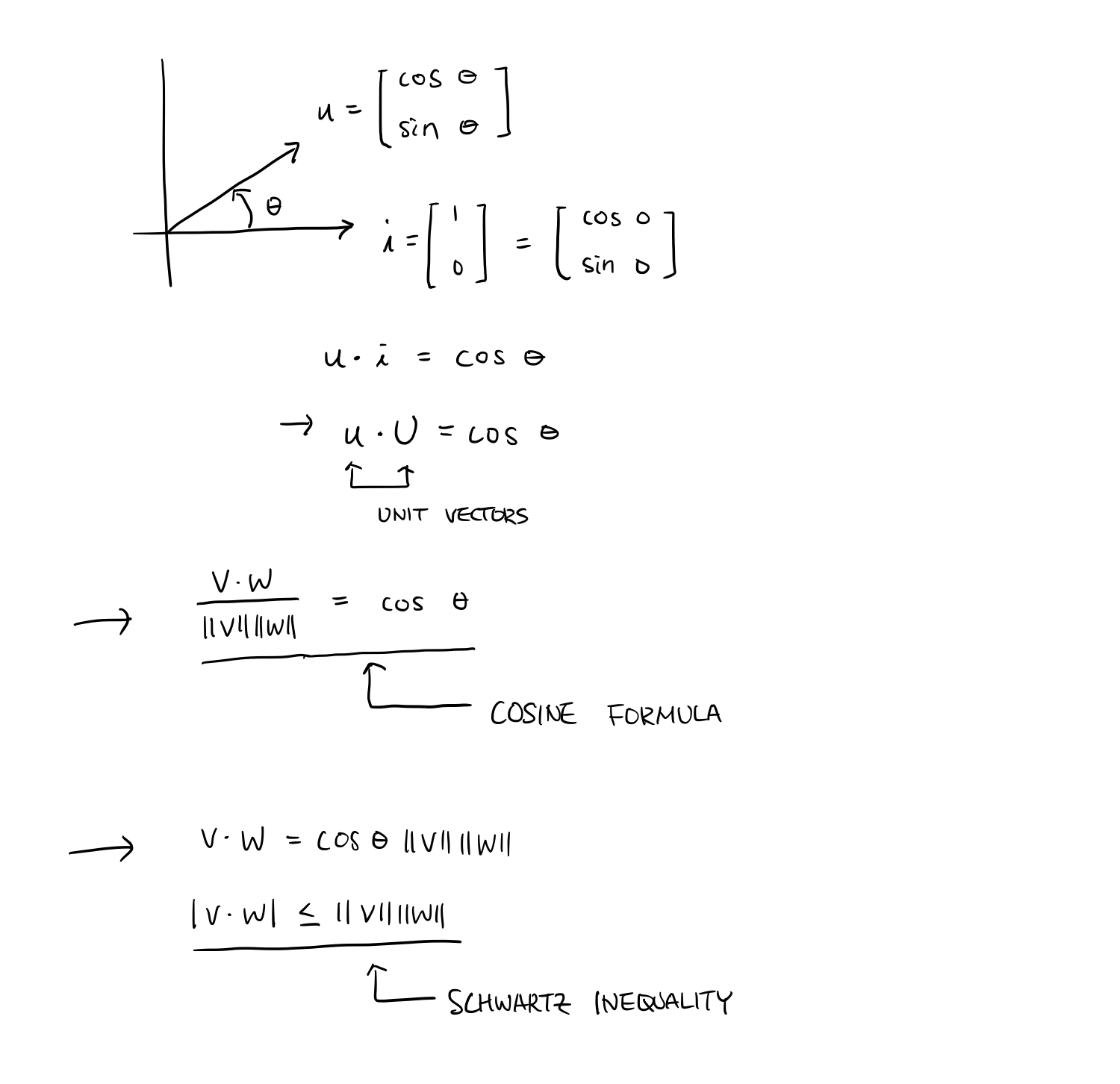
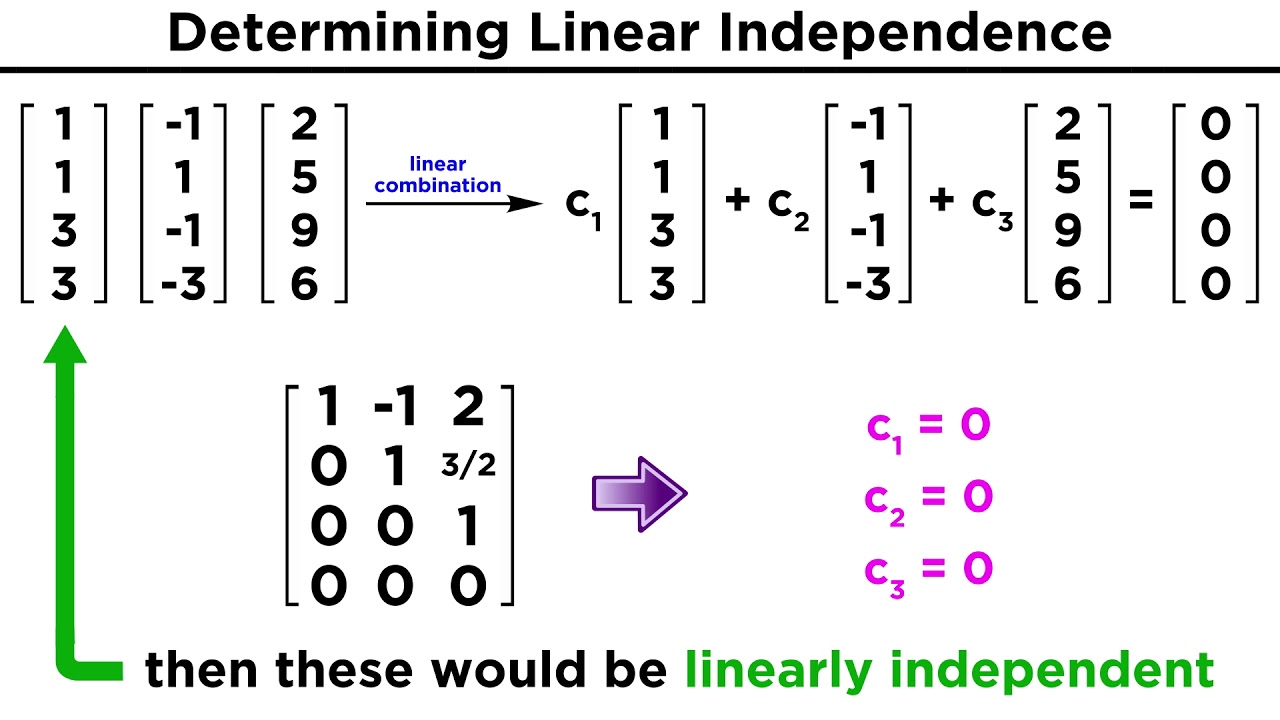
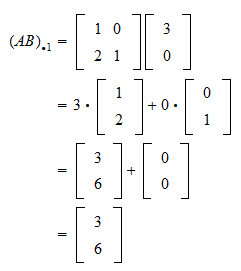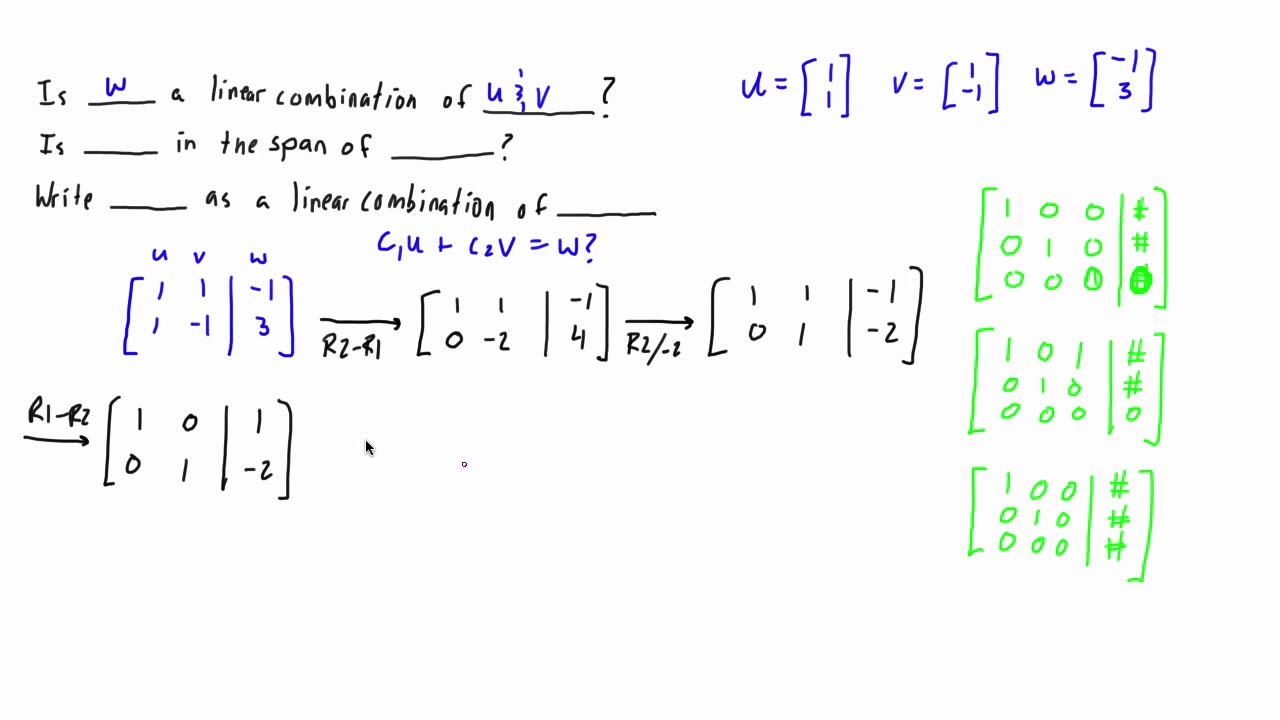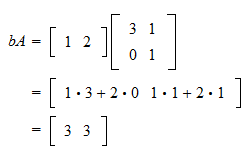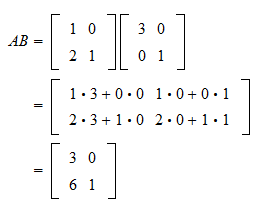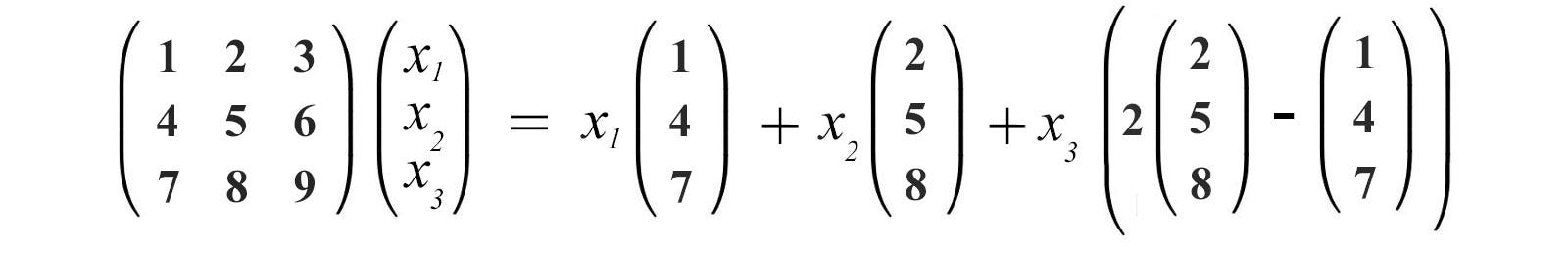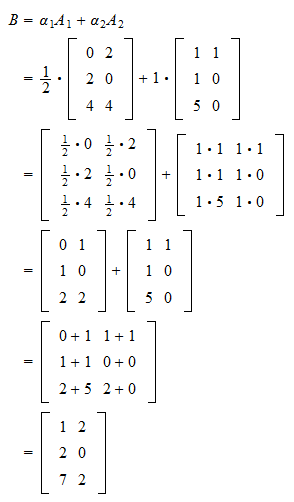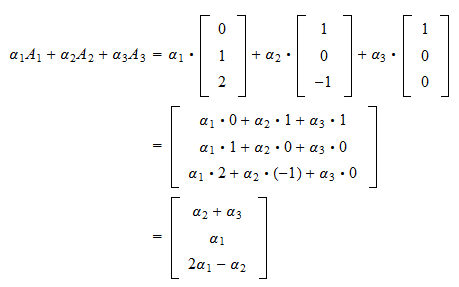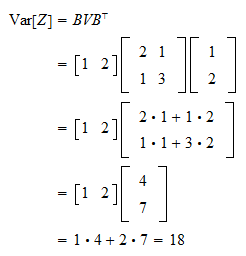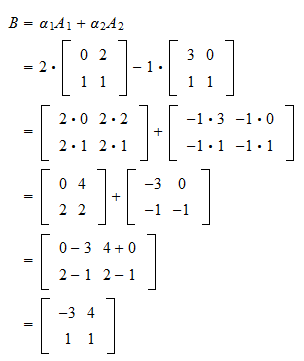Linear Combination Of Vectors Formula

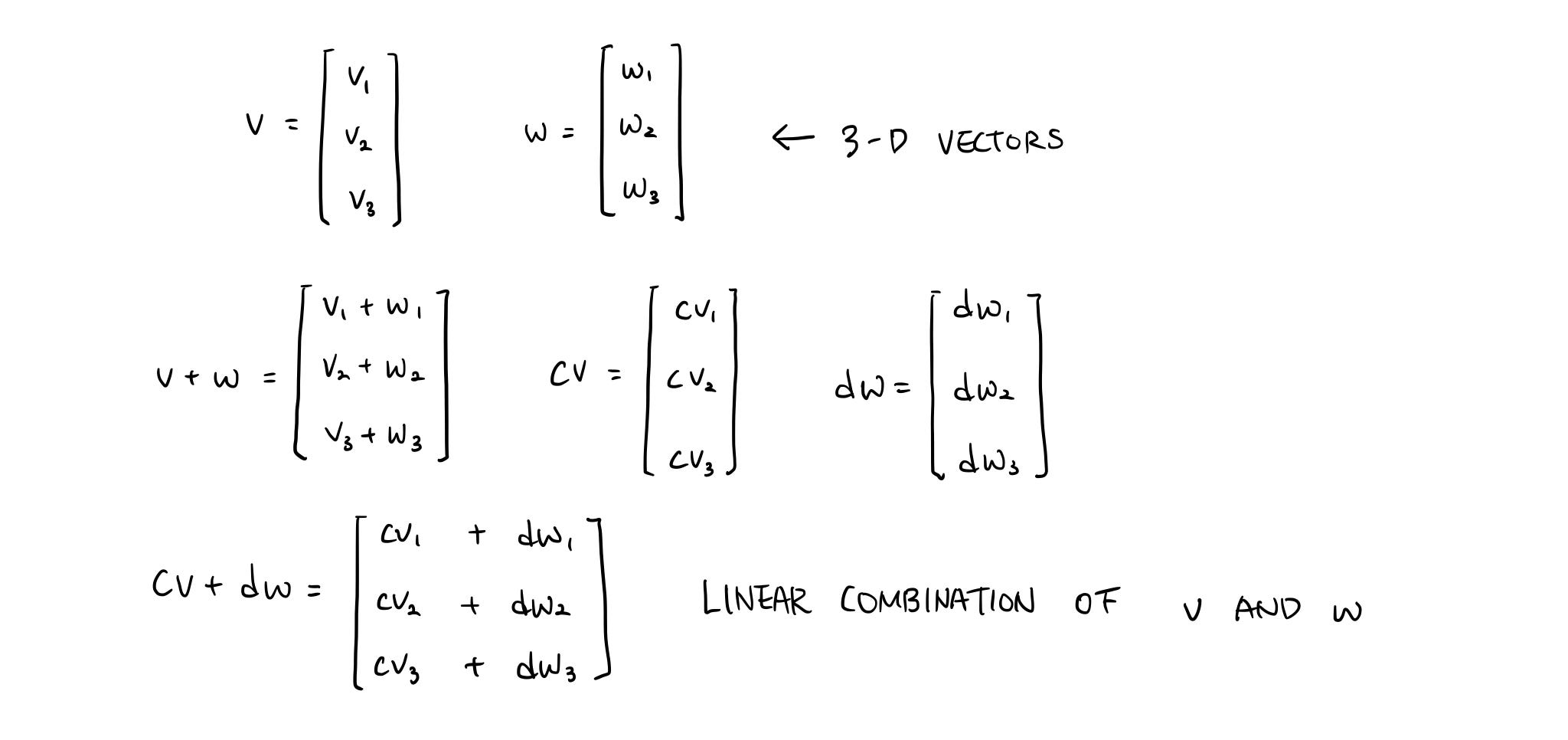
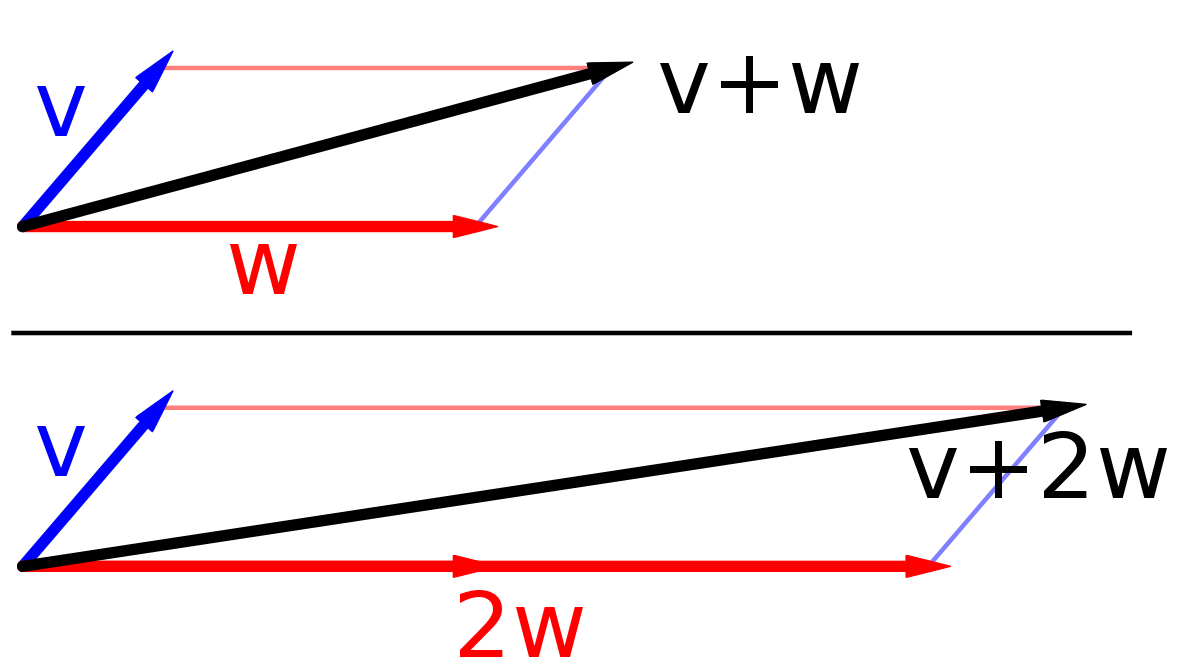
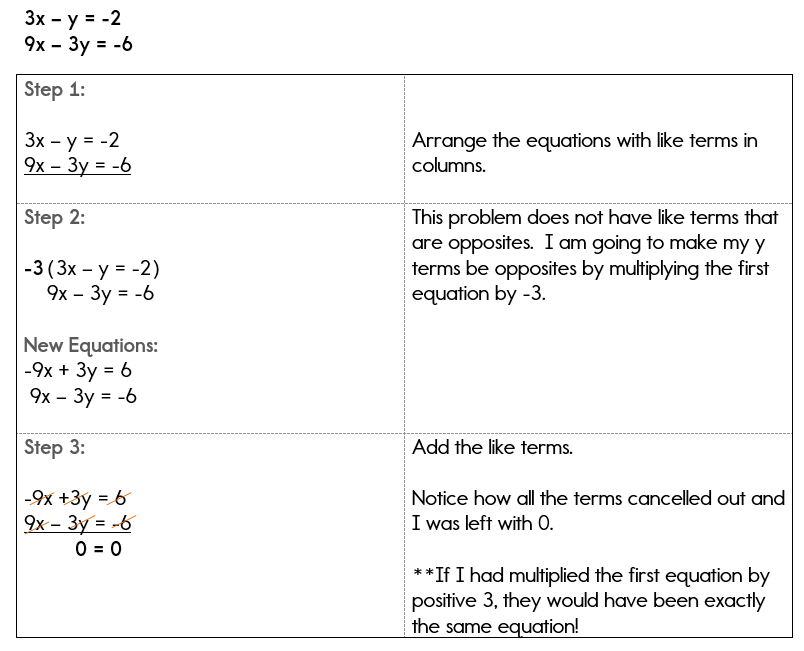
Linear combinations and span given two vectors v and w a linear combination of v and w is any vector of the form av bw where a and b are scalars.

Linear combination of vectors formula. I left langle 10 right rangle and j left langle 01 right rangle this i is always written in boldface to distinguish from the imaginary number sqrt 1. But it is actually possible to talk about linear combinations of anything as long as you understand the main idea of a linear combination. In linear algebra we define the concept of linear combinations in terms of vectors. In mathematics a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results eg.

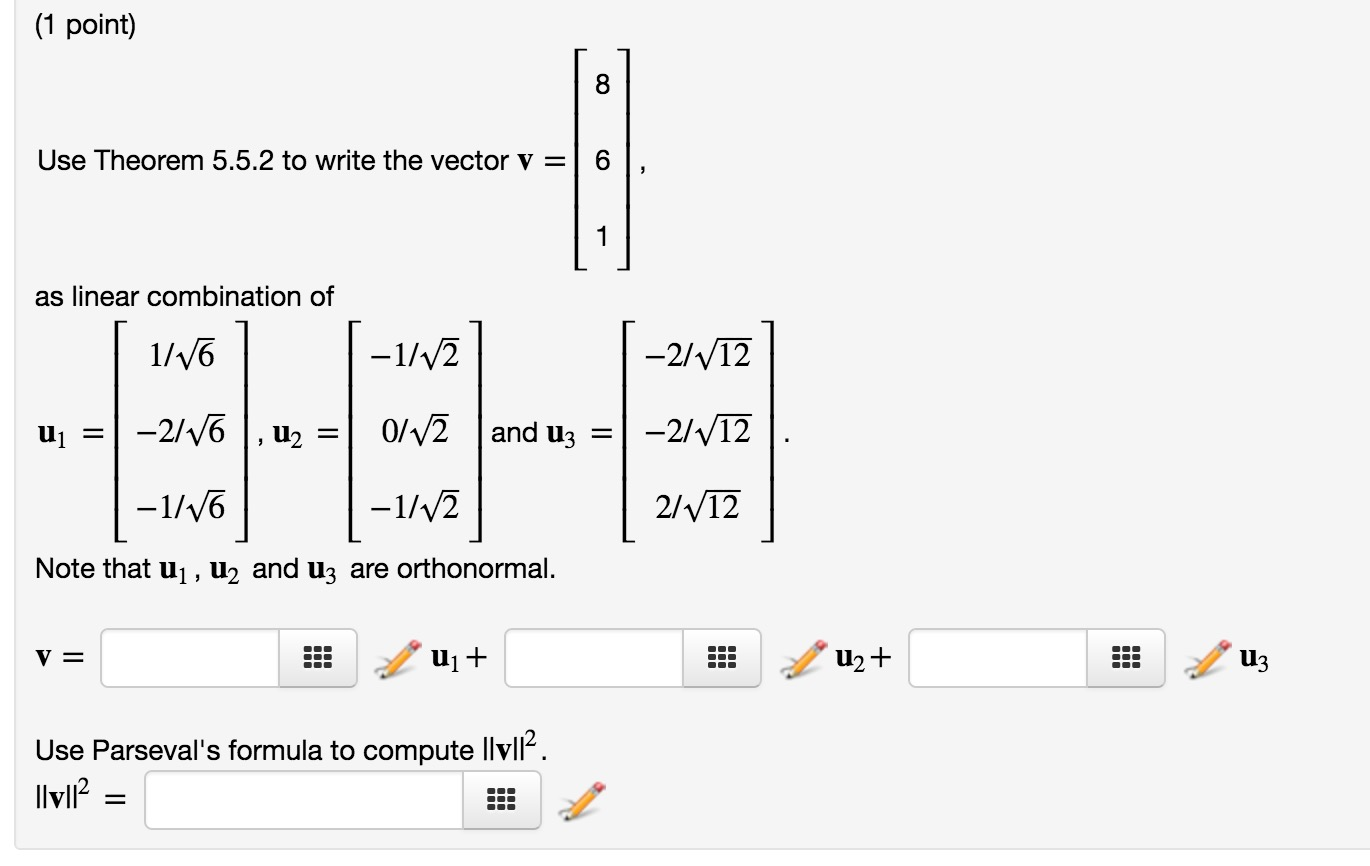
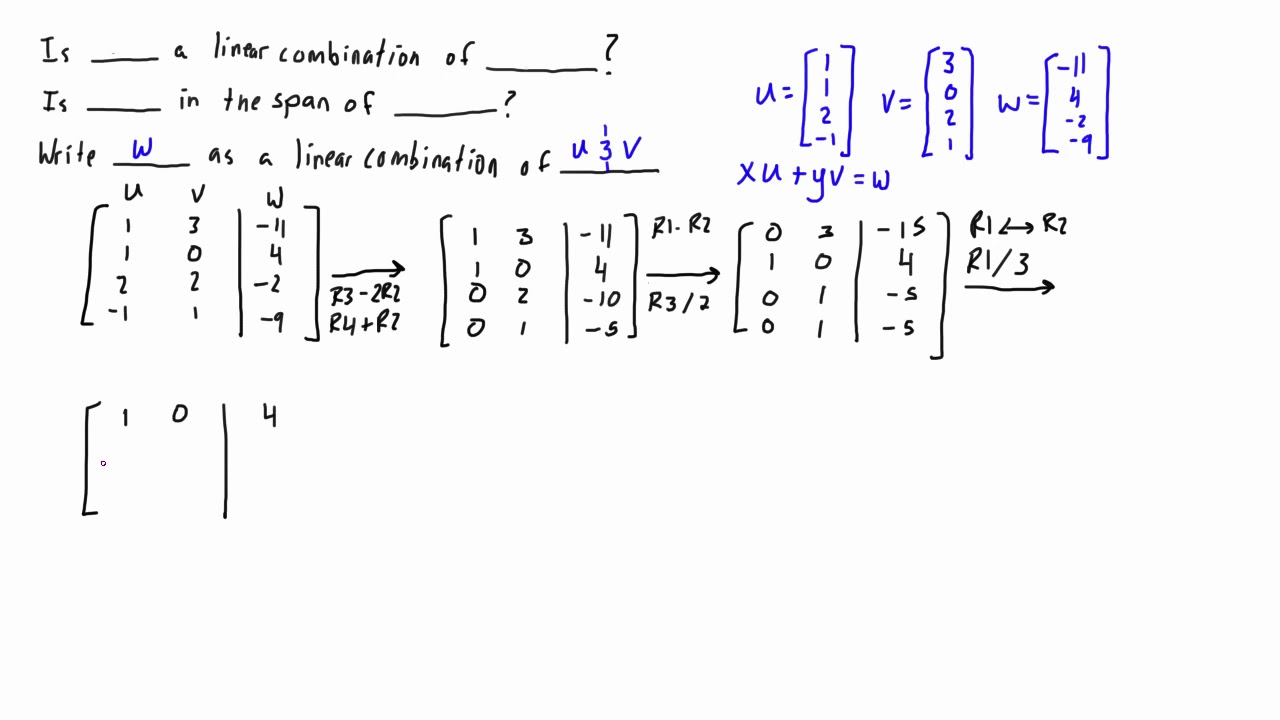
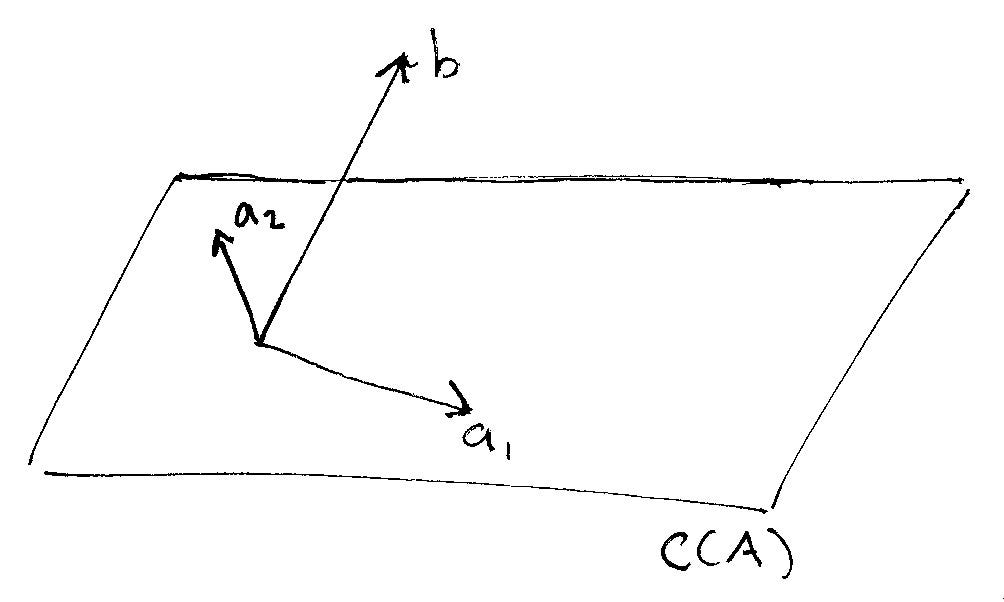
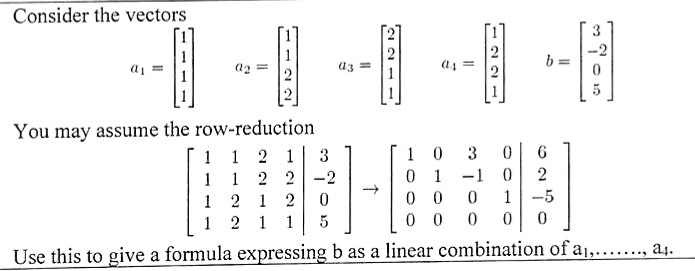
A1 a2 a3 v if this matrix represents a consistent system of equations then we can say that v is a linear combination of the other vectors. Analysis of linear dependence among v 1v 2. For example the vector 6810 is a linear combination of the vectors 111 and 123 since 2 4 6 8 10 3 5 4 2 4 1 1 1 3 5 2 2 4 1 2 3 3 5 more generally a linear combination of n. A linear combination of x and y would be any expression of the form ax by where a and b are constants.

Scalarsomething 1 scalarsomething 2 scalarsomething 3. A linear combination of v 1v 2. Enter your vectors horizontal with components separated by commas. Thus v 1 is shown to be a linear combination of the remaining vectors.

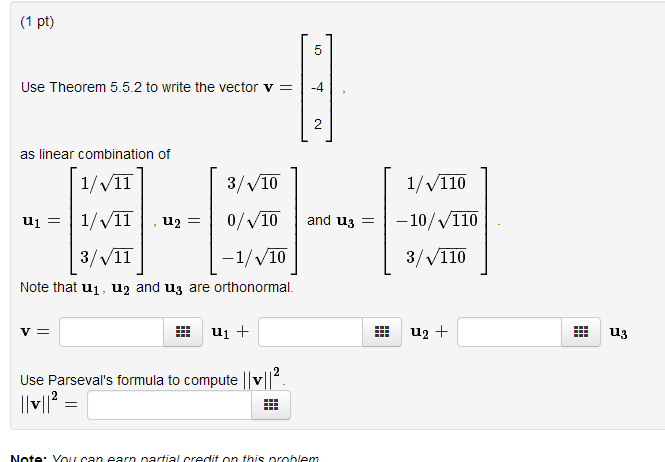
Examples v 1 v 2 then choose what you want to compute. U orthogonal complement of v 1v 2. Linear combination of unit vector let us consider standard unit vectors left langle 10 right rangle and left langle 01 right rangle.