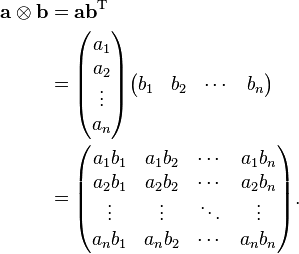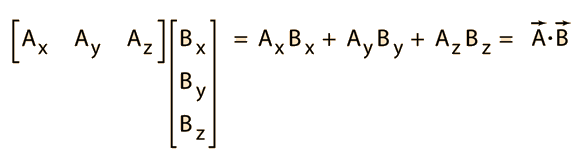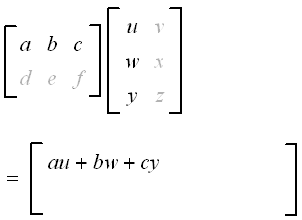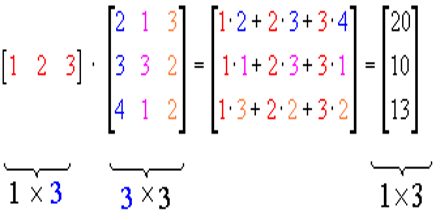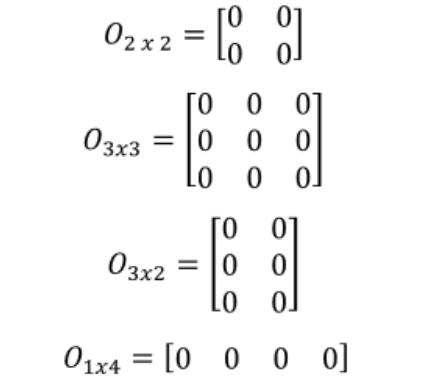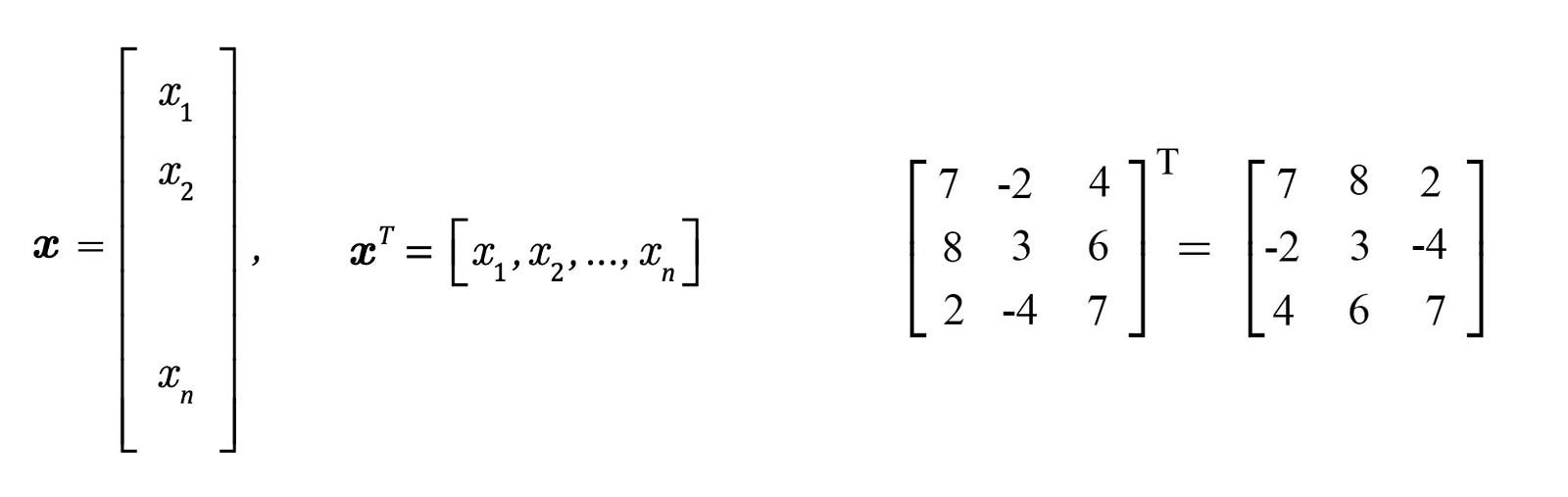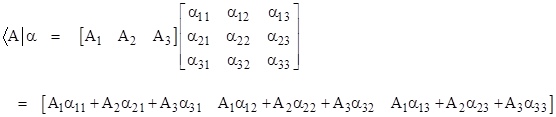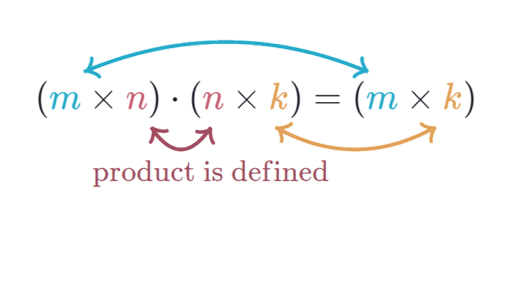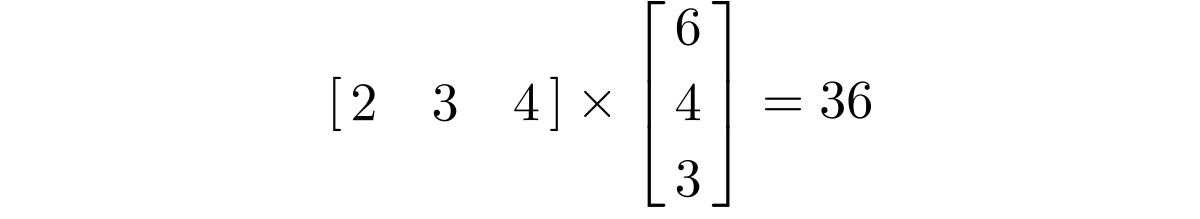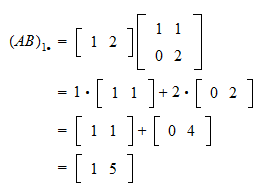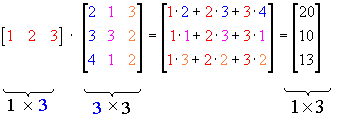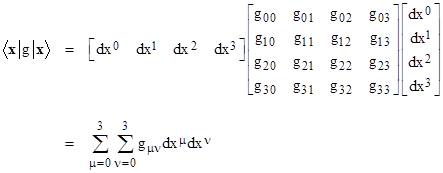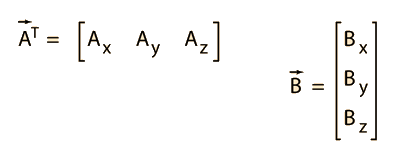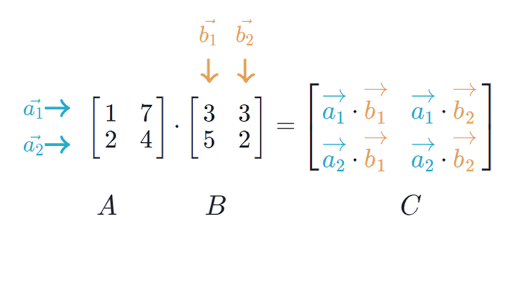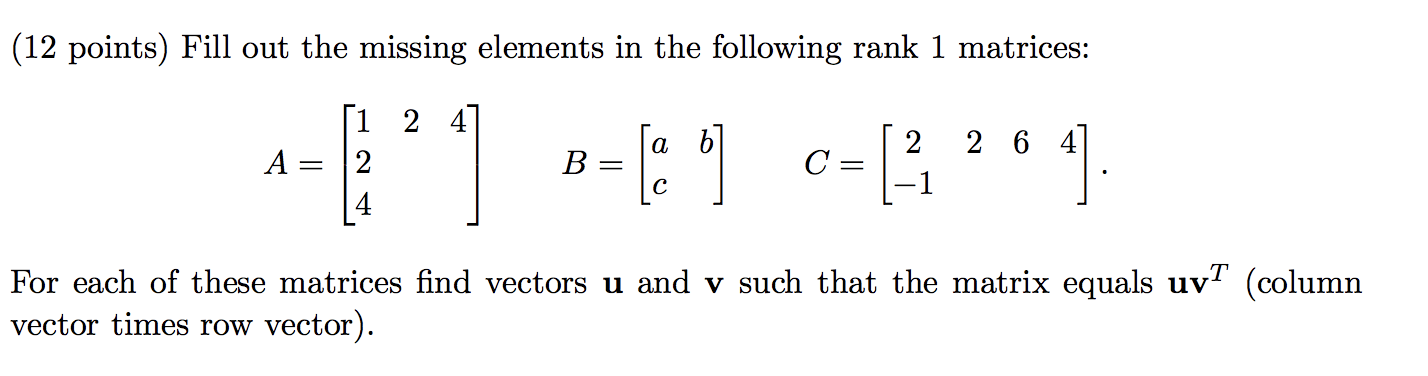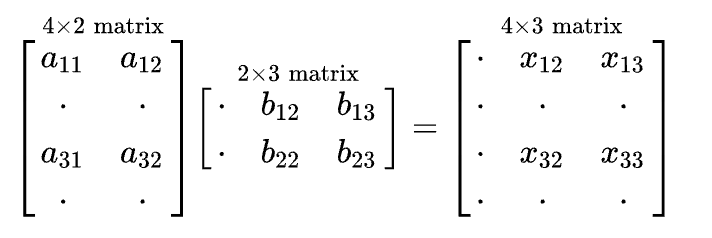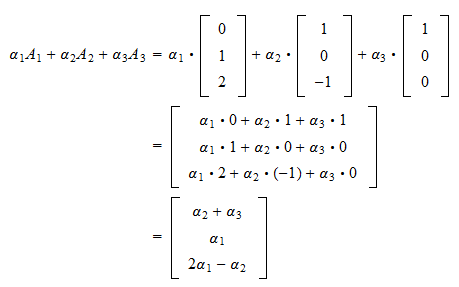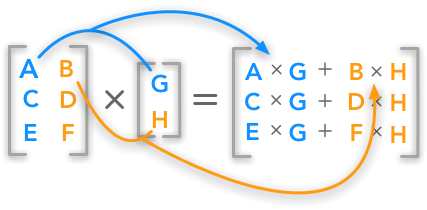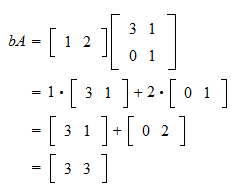Row Vector Times Matrix

Similarly a row vector or row matrix is a 1 m matrix that is a matrix consisting of a single row of m elements. Vector matrix multiplication row wise follow 306 views last 30 days kamuran on 16 sep 2015. To multiply a row vector by a column vector the row vector must have as many columns as the column vector has rows.
row vector times matrix row vector times matrix times column vector

The transpose of a matrix.

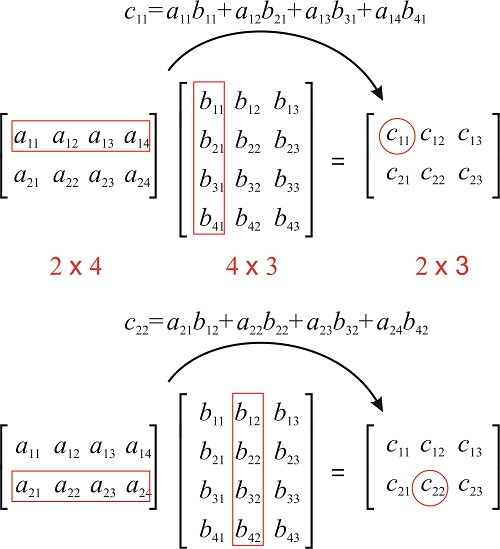
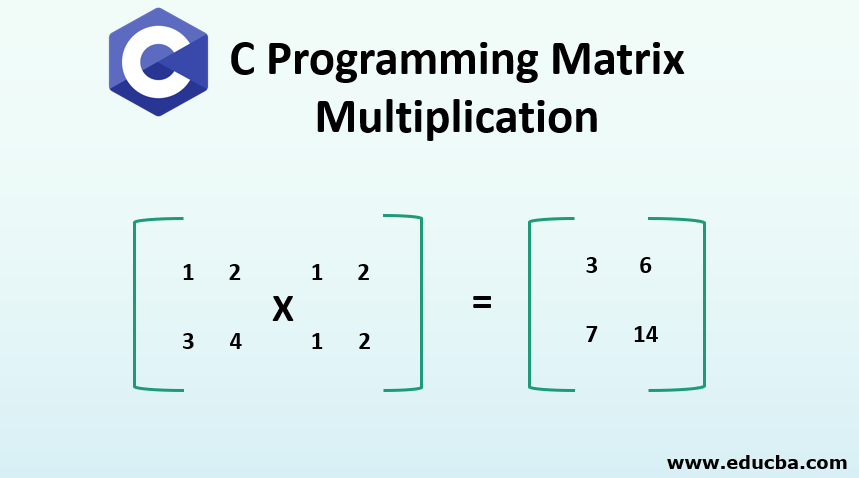
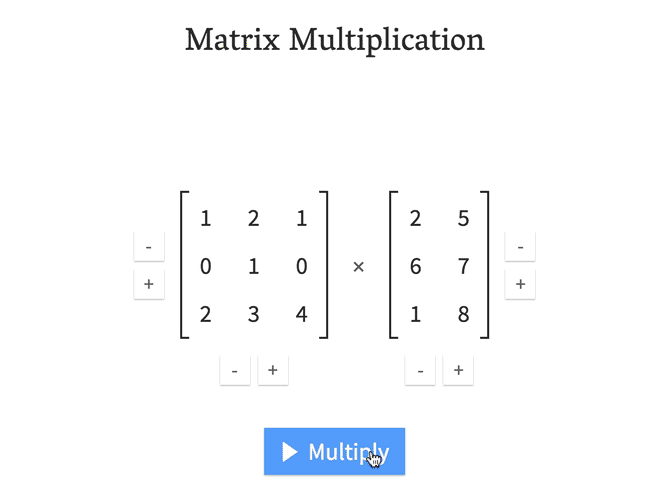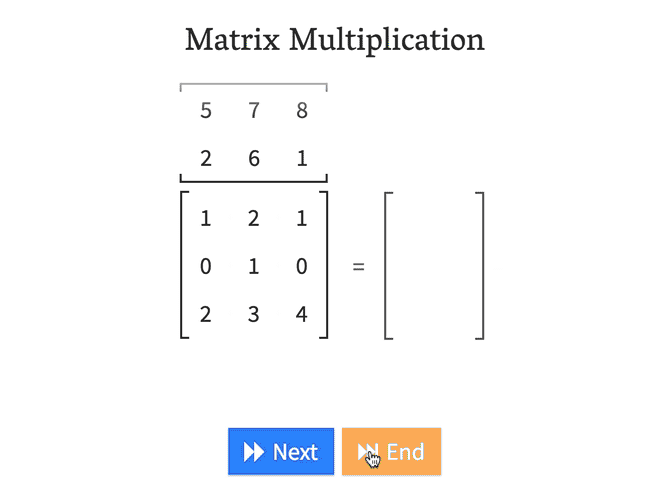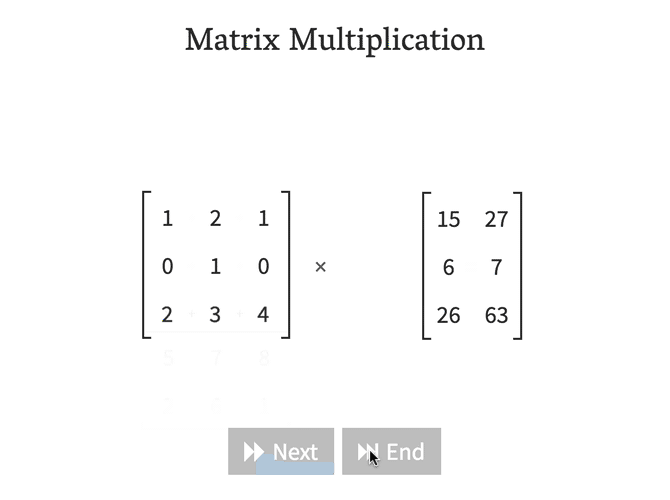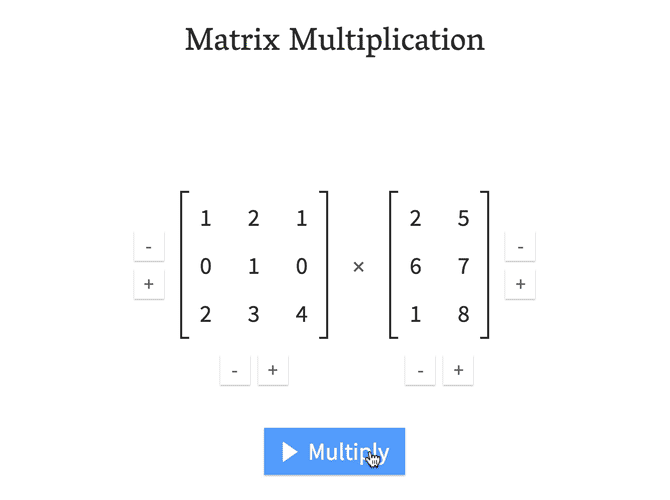
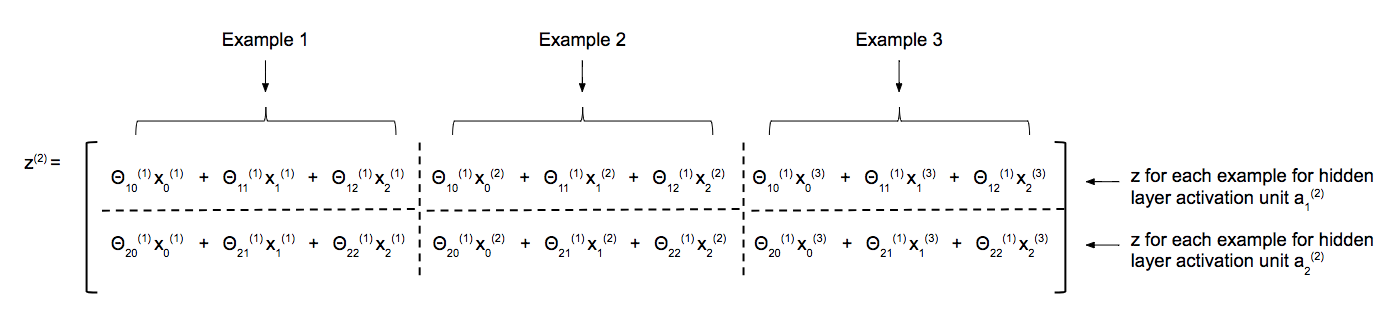
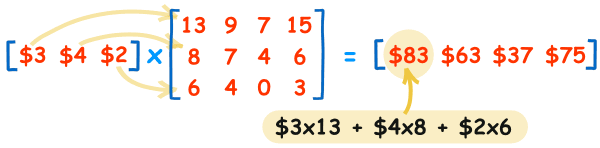
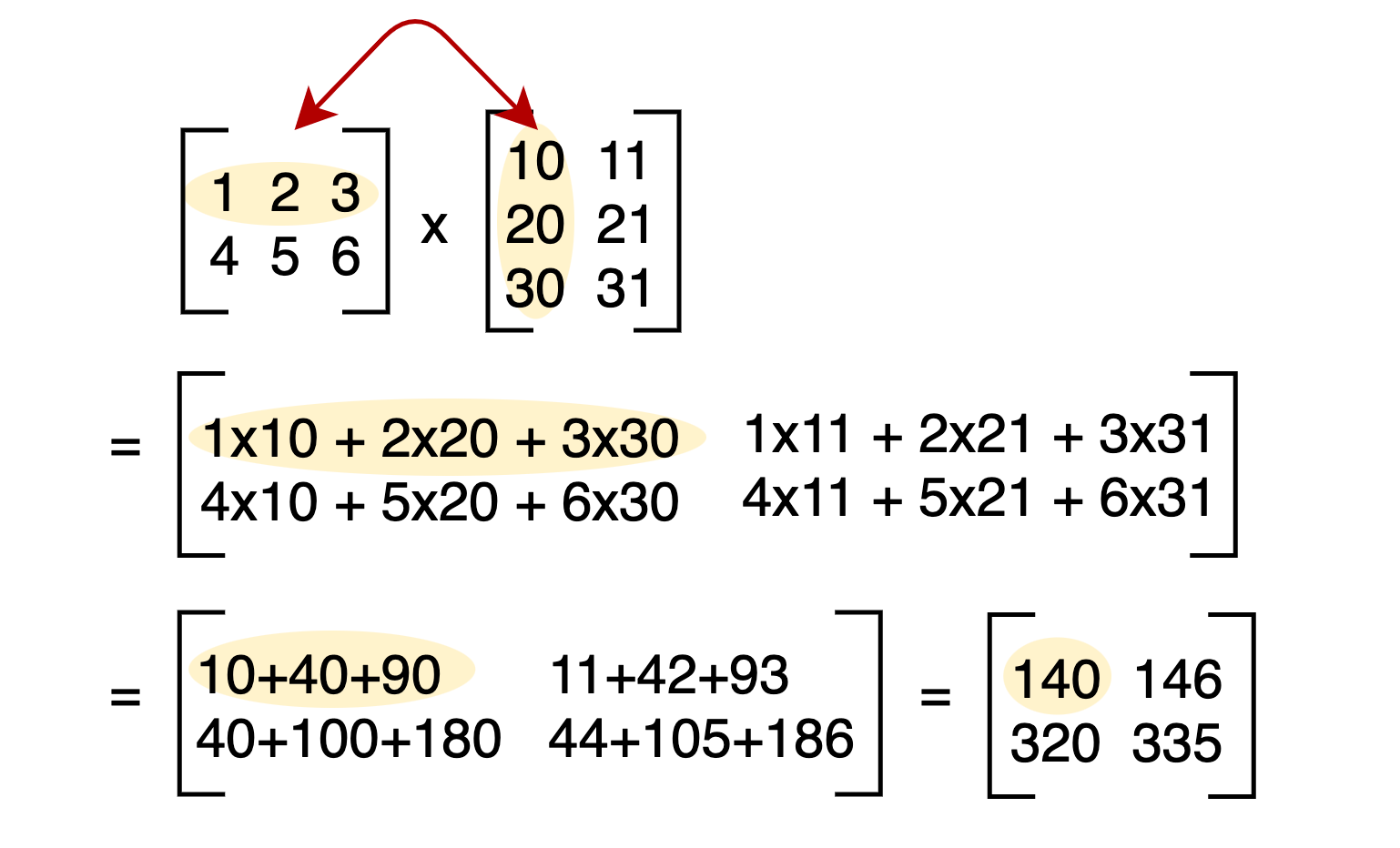
Row vector times matrix. Matrix and vector multiplication examples. Let us define the multiplication between a matrix a and a vector x in which the number of columns in a equals the number of rows in x. Matrix and vector multiplication examples. These are the calculations.

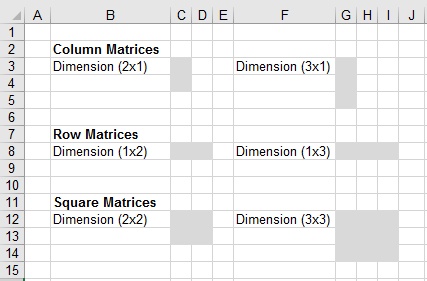
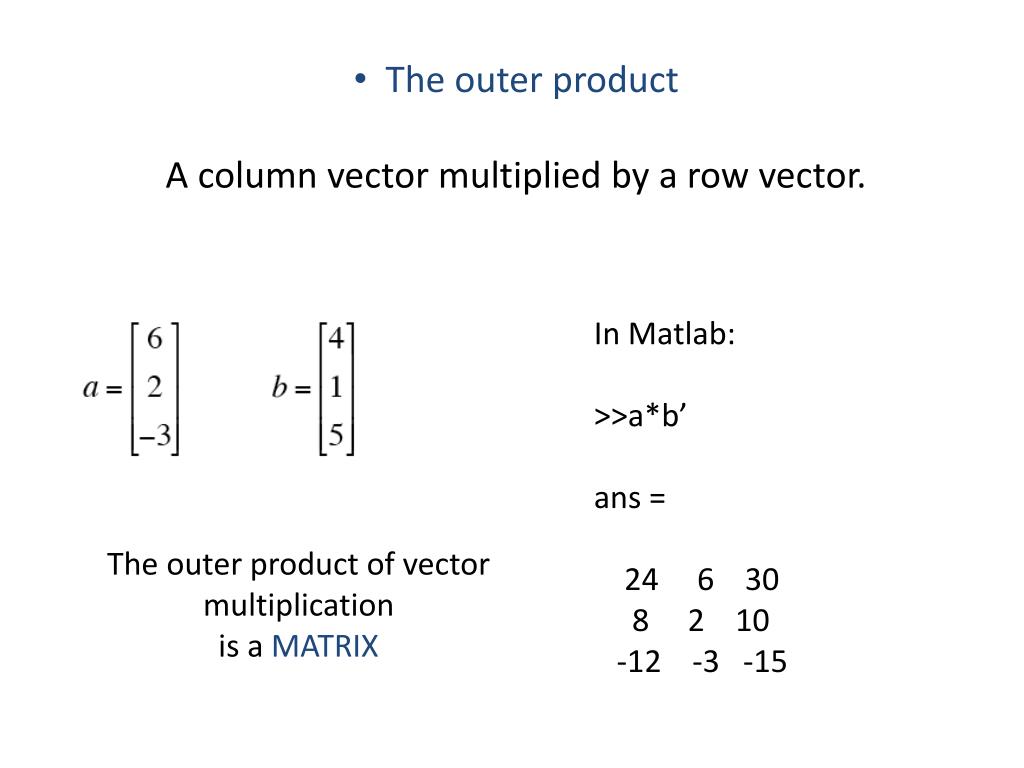
Now the columns or rows can be omitted and they will be calculated by r however the one given needs to be a multiple of the total number of elements. So if a is an m n matrix then the product a x is defined for n 1 column vectors x. For matrix multiplication the number of columns in the first matrix must be equal to the number of rows in the second matrix. In linear algebra a column vector or column matrix is an m 1 matrix that is a matrix consisting of a single column of m elements.

Noah tang on 28 oct 2019 accepted answer. The transpose indicated by t of a row vector is a column vector. Math 2241 spring 2020. The result matrix known as the matrix product has the number of rows of the first and the number of columns of the second matrix.

I dont really want to use for loop for that ie. Multiplying a vector by a matrix. Hi i need to multiply each row of very large matrix with a row of corresponding vector. Matrix multiplication in r setup matrixc1538 ncol2 nrow2 1 2 1 1 3 2 5 8.

We call the number 2 in this case a scalar so this is called scalar multiplication. When doing matrix multiplications you need to insure that you match the dimensions. Throughout boldface is used for the row and column vectors. In mathematics matrix multiplication is a binary operation that produces a matrix from two matrices.

Their dimension do not match and therefore you cannot multiply them. This one has 2 rows and 3 columns to multiply a matrix by a single number is easy. Similary a row vector also is a special matrix which is 1 n. For example say you have 2 matrices a and b of respective dimensions 3 4 and 2 5.

The dimension of the resultant matrix will always have the of rows of the first matrix and the of columns of the second matrix. Matrix and vector multiplication examples.