Sparse Matrix Vector Multiplication Parallel

22 sparse matrix vector multiplication sparse matrix vector multiplications are the dominant components of both petsc krylov space iterative solvers and many precon ditioners used together with the solvers such as multigrid and polynomial preconditioners. An outer product based sparse matrix multiplication accelerator subhankar pal jonathan beaumont dong hyeon park aporva amarnath siying feng chaitali chakrabarti hun seok kim david blaauw trevor mudge ronald dreslinski university of michigan ann arbor mi arizona state university tempe az subh jbbeau dohypark aporvaa fengsy hunseok. Nnz number of non zero values n dimension of matrix row access is easy but column access difficult.
sparse matrix vector multiplication parallel

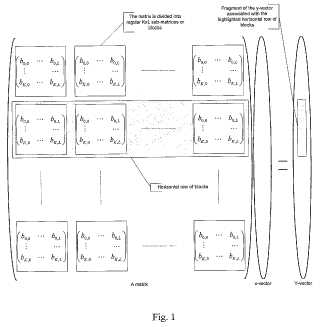
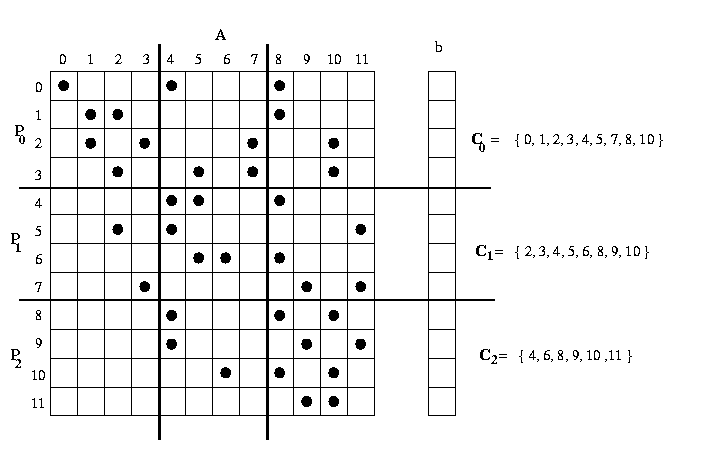
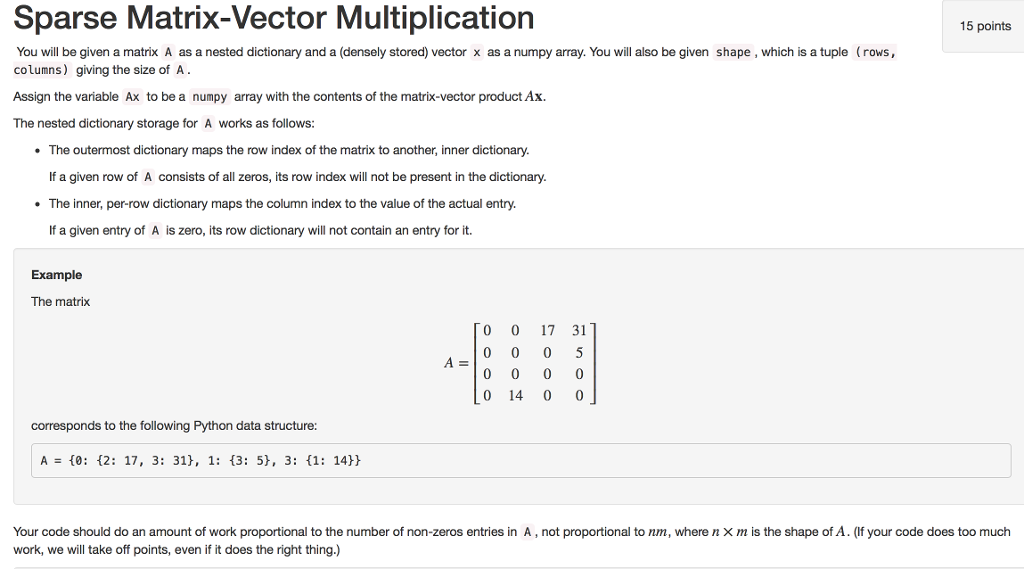
In the sparse matrix vector multiplication consider the characteristic of sparse matrix partition the matrix into sub matrix every slave will do the several sub matrix of multiplication simultaneously and then send all the results back to master processor.

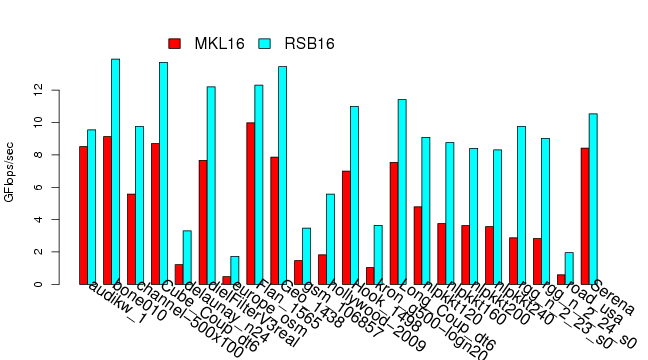
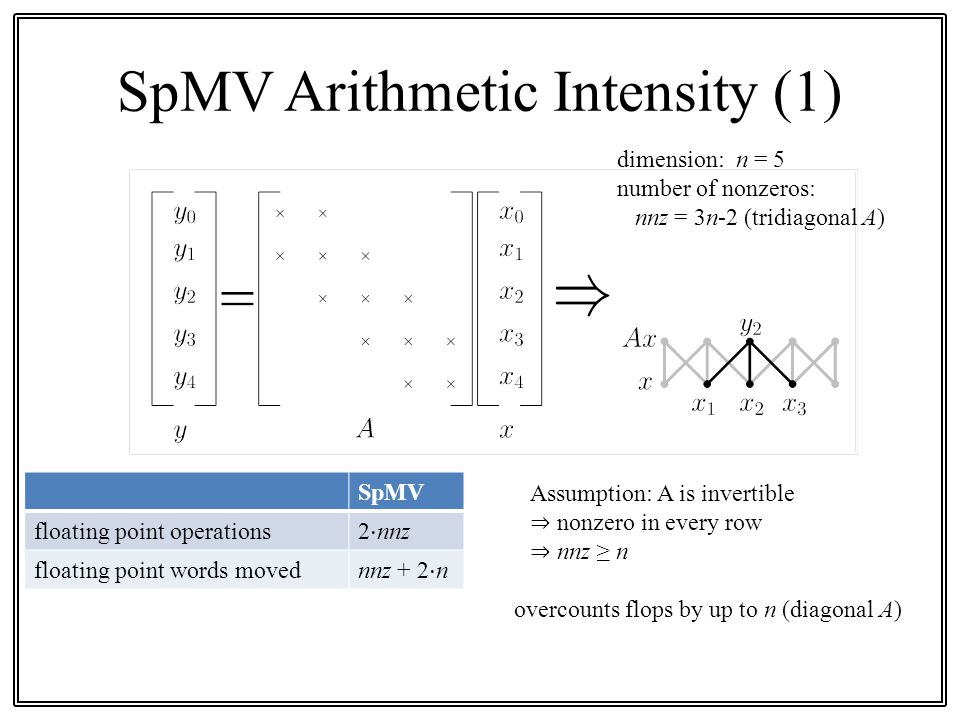
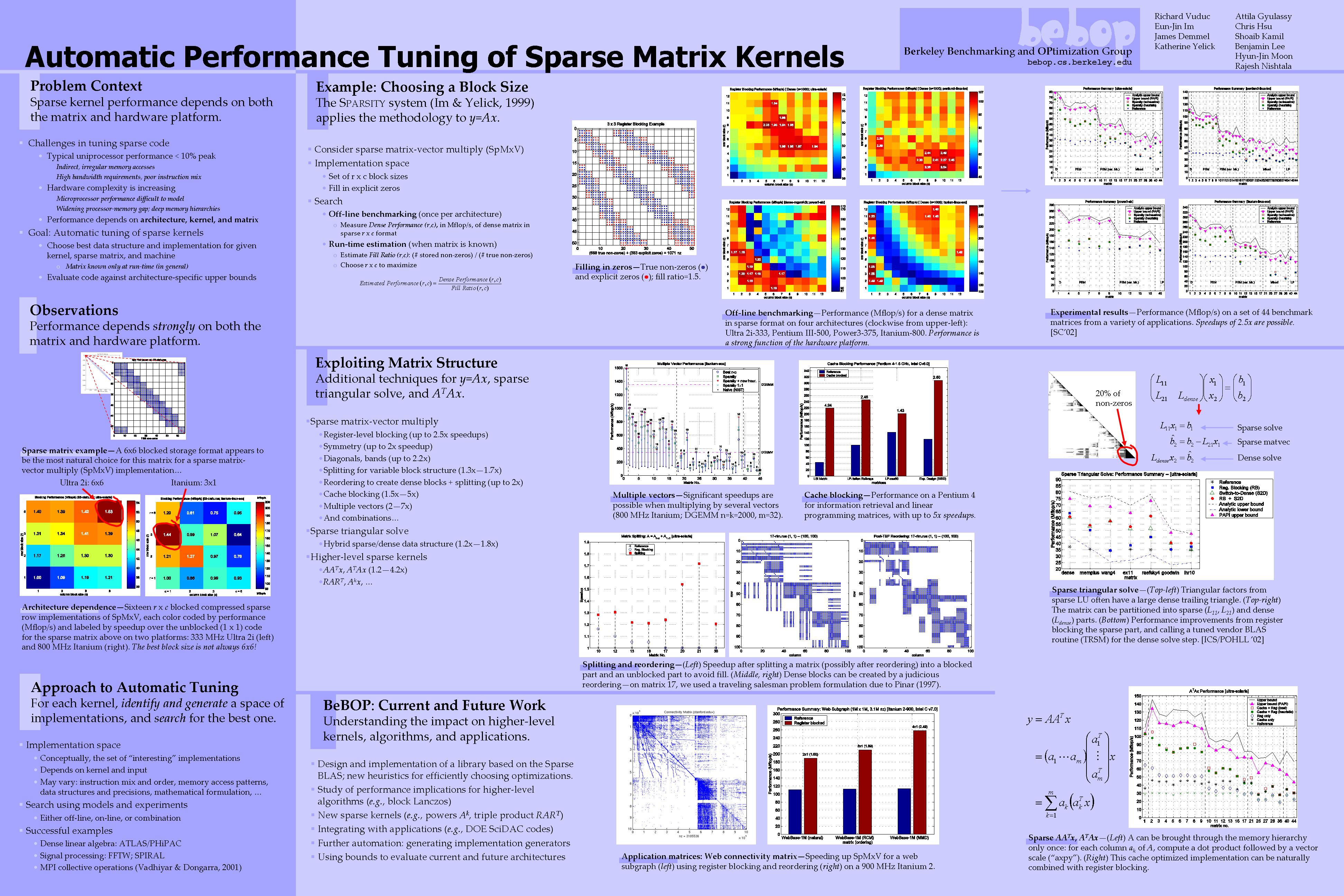
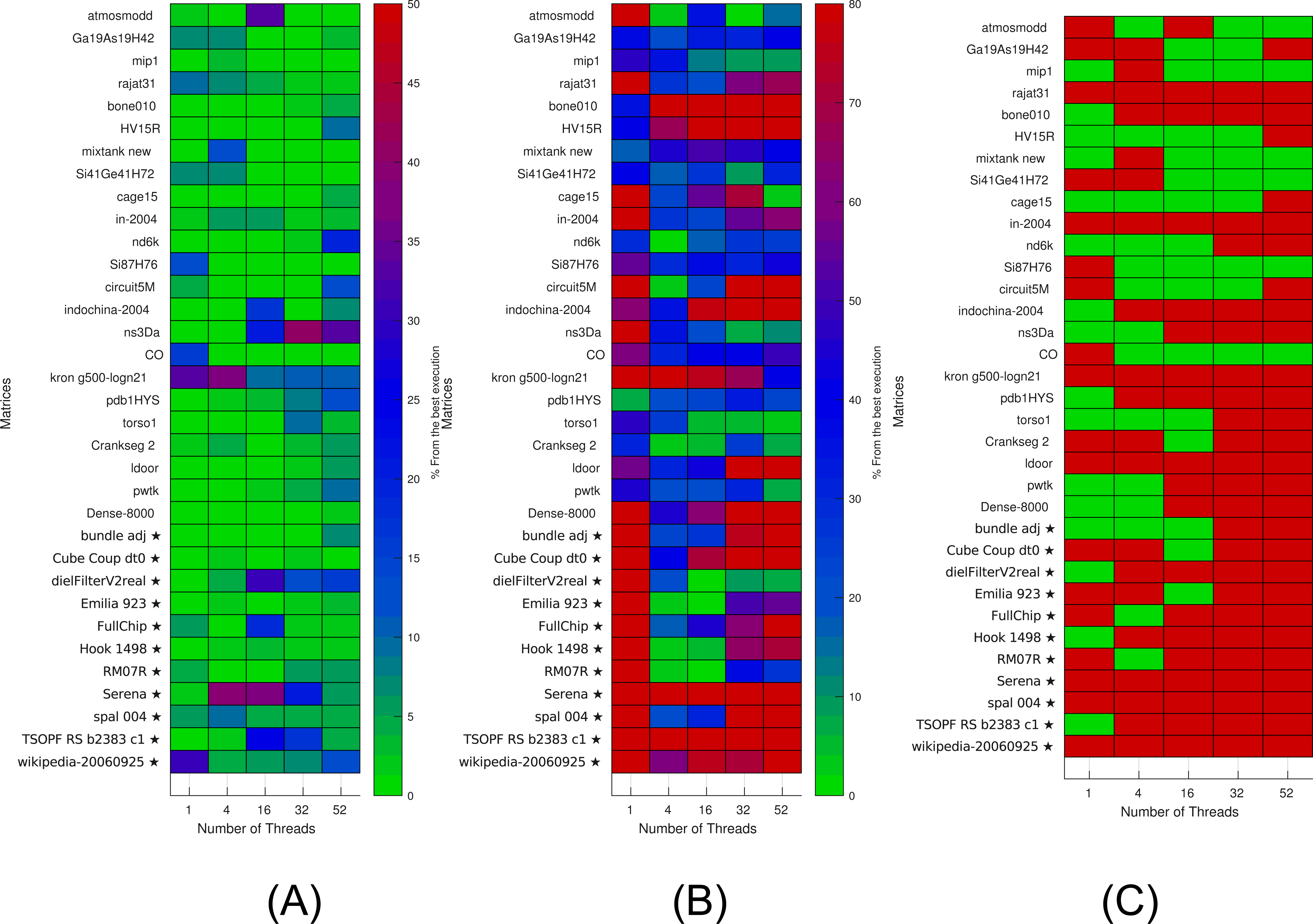
Sparse matrix vector multiplication parallel. Sparse matrix vector multiplication spmv of the form displaystyle yax is a widely used computational kernel existing in many scientific applications. There exist different classes of parallel problems embarrassingly parallel sparse matrix vector multiplication memory bound address coalescing of memory accesses static parallelism sparse triangular solve parallelism bound predict it ahead of time. Our algorithm operates directly upon the compressed sparse row csr sparse matrix format without preprocessing inspection reformatting or supplemental encoding. Abstractwe present a strictly balanced method for the parallel computation of sparse matrix vector products spmv.

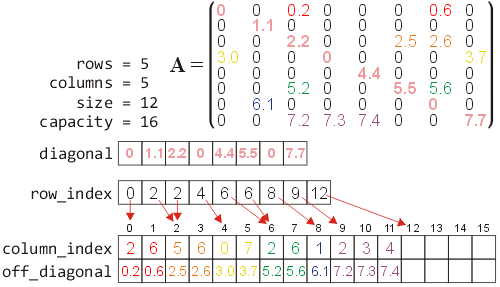
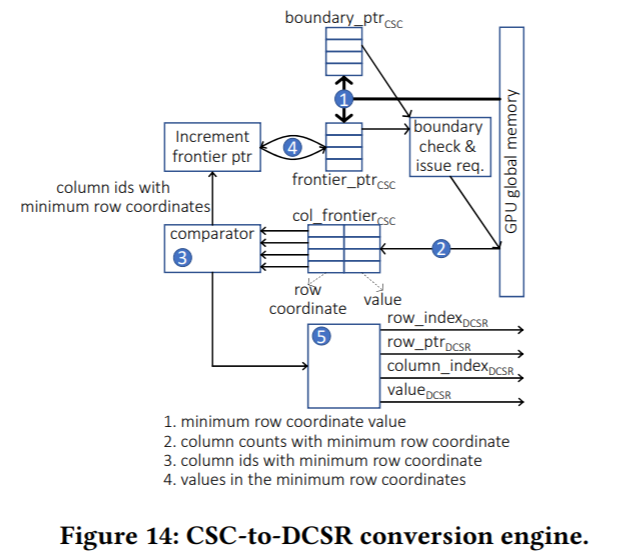
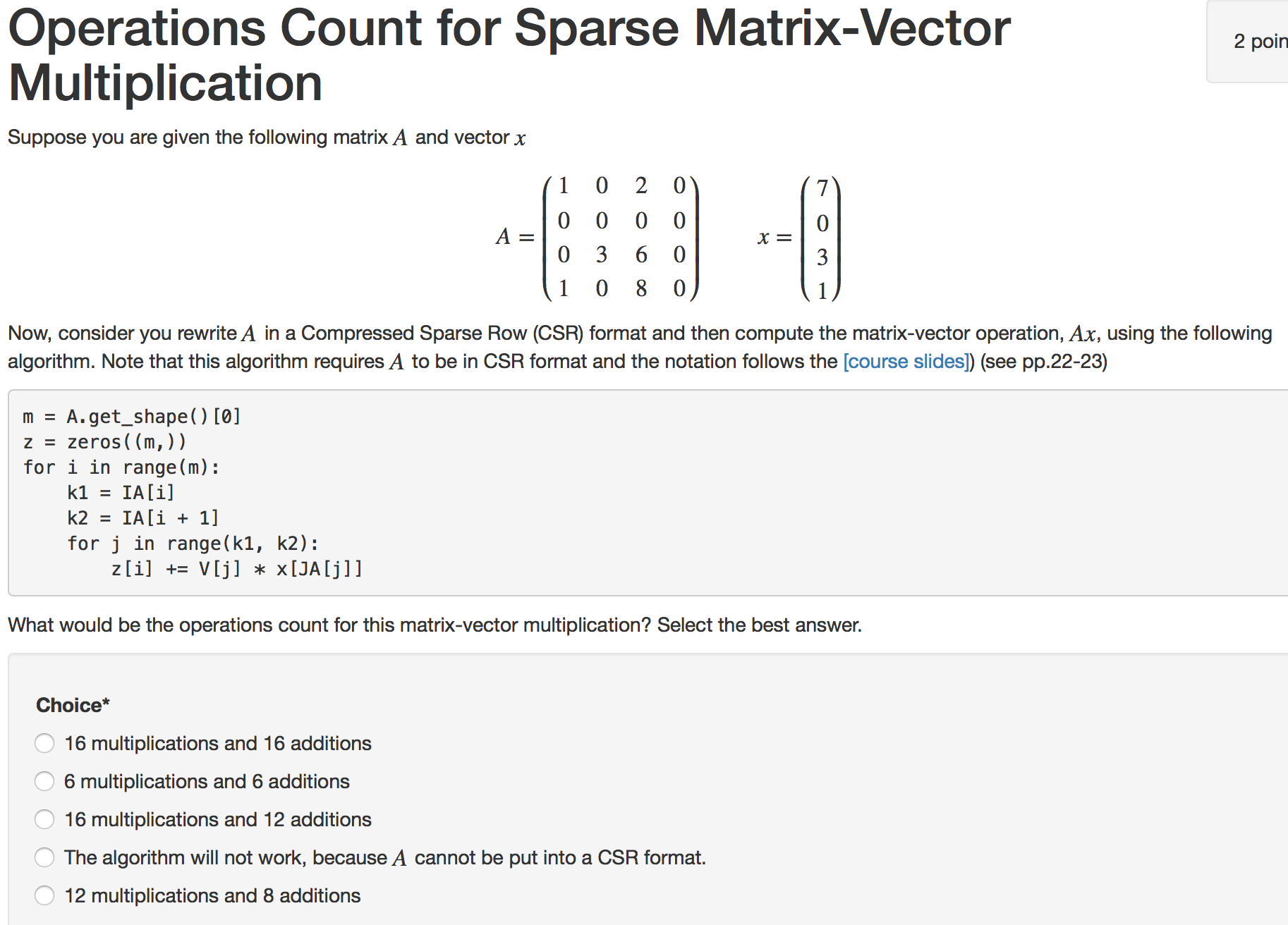
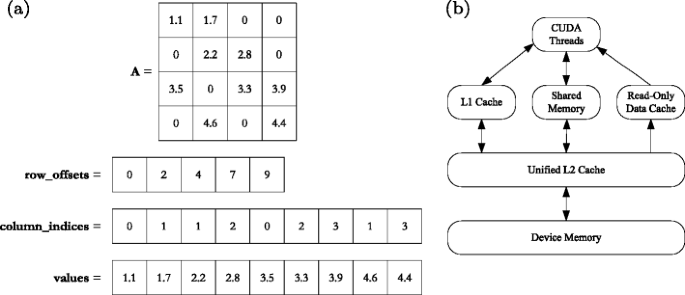
Moreover since matrix vector multiplication for sparse matrices is generally limited by memory bandwidth it is desirable to nd a storage format for which both ax and atx can be computed in parallel without performing more than nnz fetches of nonzeros from the memory to compute either product. Matrix vector multiplication in the compressed sparse row method. In parallel each process owns a consecutive row block of the matrix and a portion of. The following code fragment performs the matrix vector multiplication when the matrix is stored using the compressed sparse row method.

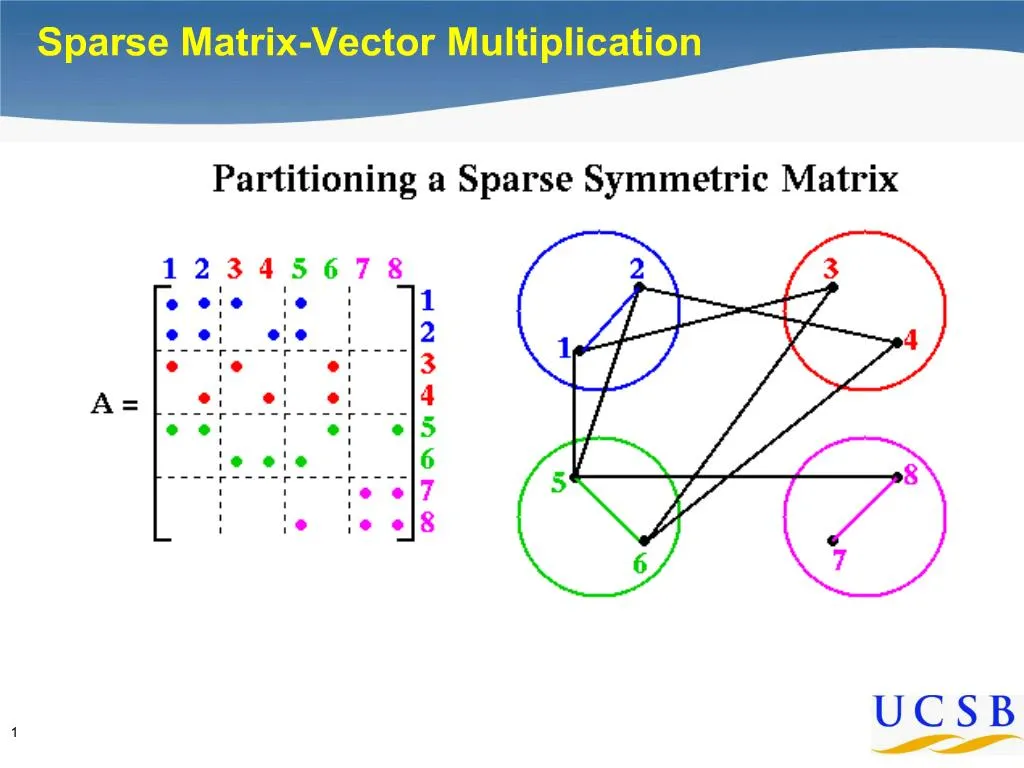
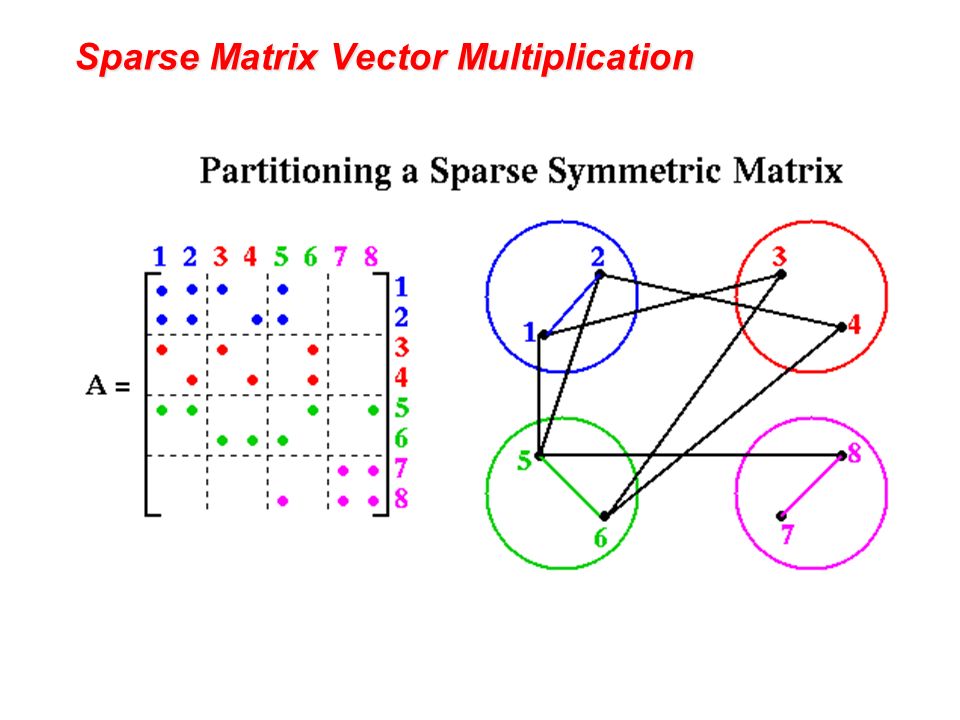
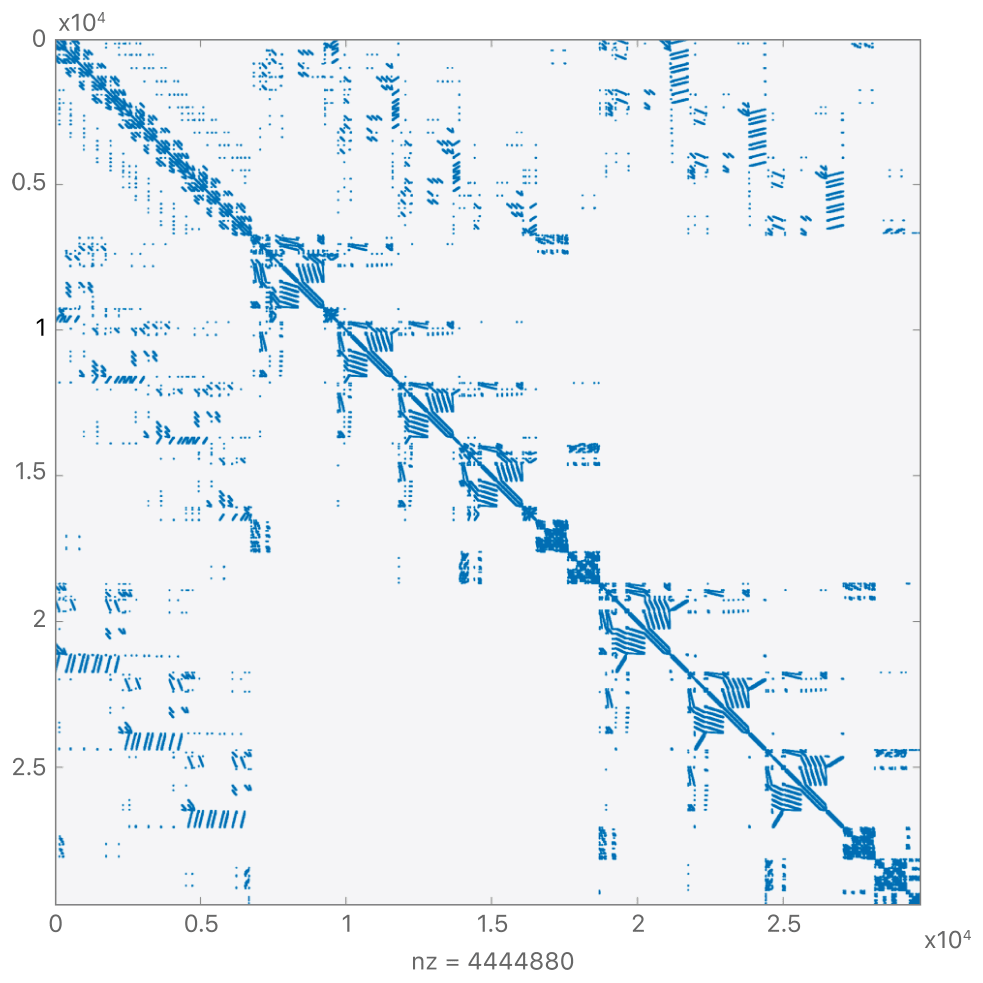
Sparse matrix is a representation of a sparse graph matrix entries are edge weights number of nonzeros per row is the vertex degree edges represent data dependencies in matrix vector multiplication.