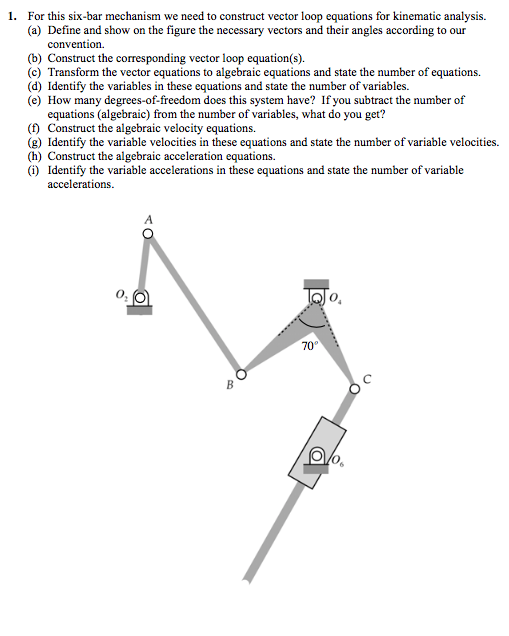
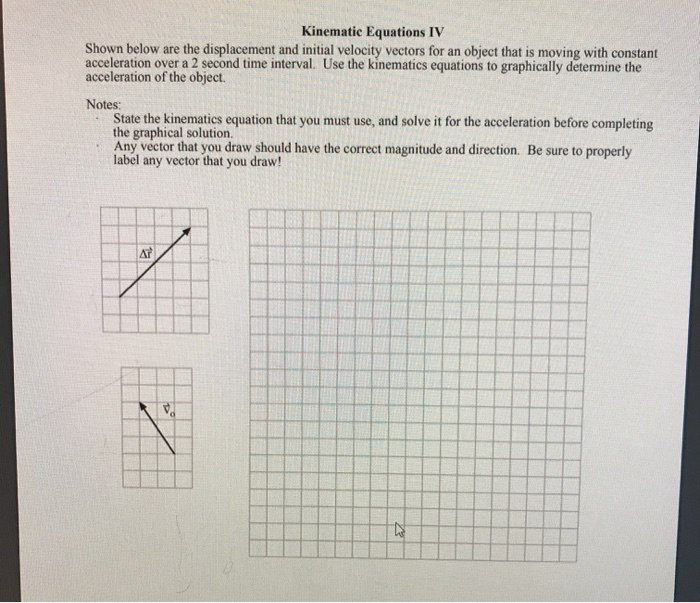
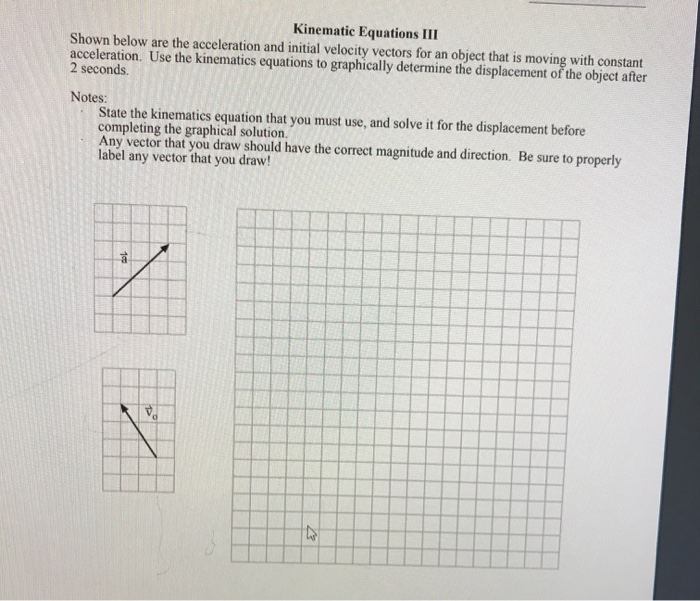
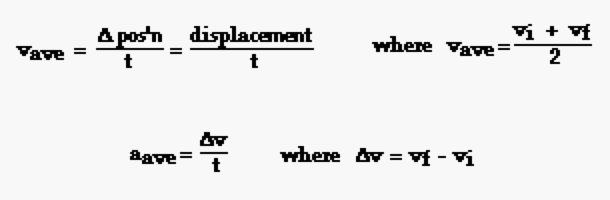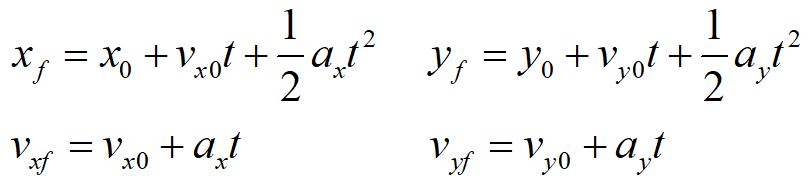Vector Kinematics Equations
The physics classroom tutorial presents physics concepts and principles in an easy to understand language.
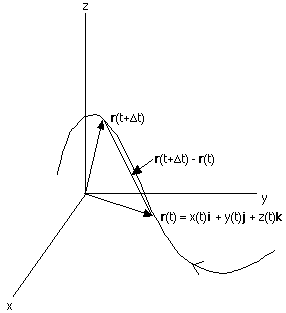
Vector kinematics equations. The vector rt. Each lesson includes informative graphics occasional animations and videos and check your understanding sections that allow the user to practice what is taught. X vot a t2. B at t0 a6i5 ms2.
The equations of translational kinematics can easily be extended to planar rotational kinematics for constant angular acceleration with simple variable exchanges. If values of three variables are known then the others can be calculated using the equations. Displacement denoted by dx initial velocity final velocity denoted by time interval denoted by constant acceleration denoted by. It follows from 21145 that r.
When it passesthrough the xaxis a216i3 ms2. Each equation contains four variables. Kinematic equations relate the variables of motion to one another. These equations link five kinematic variable.
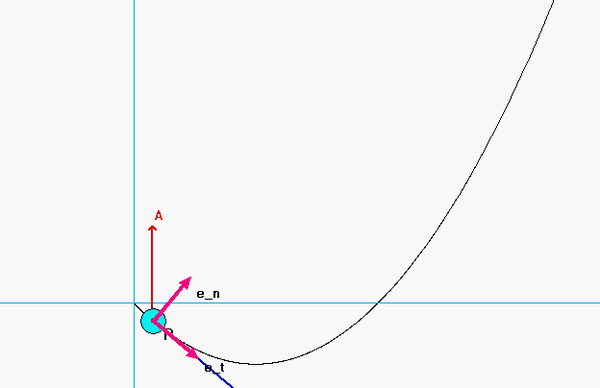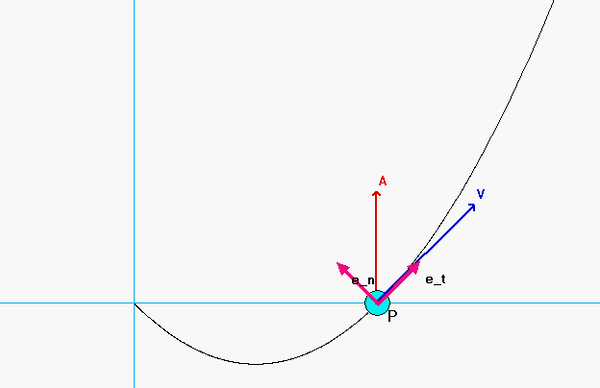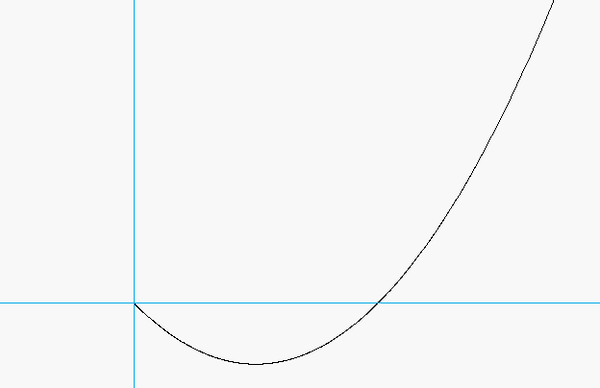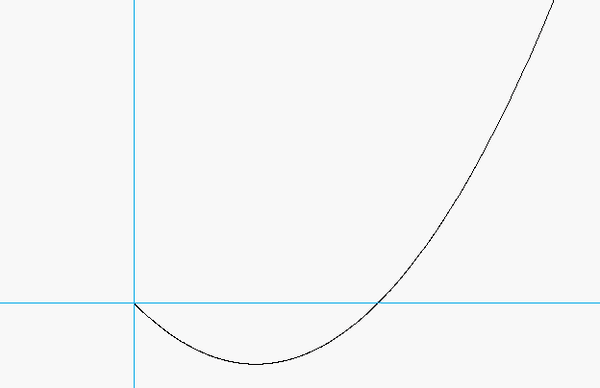
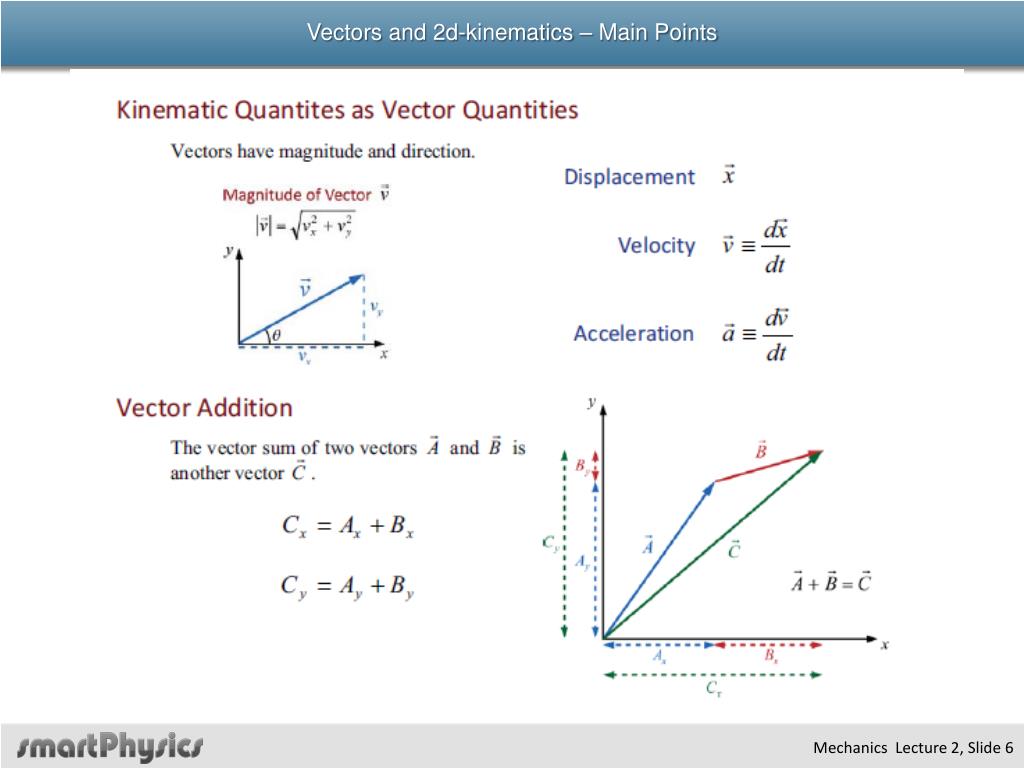
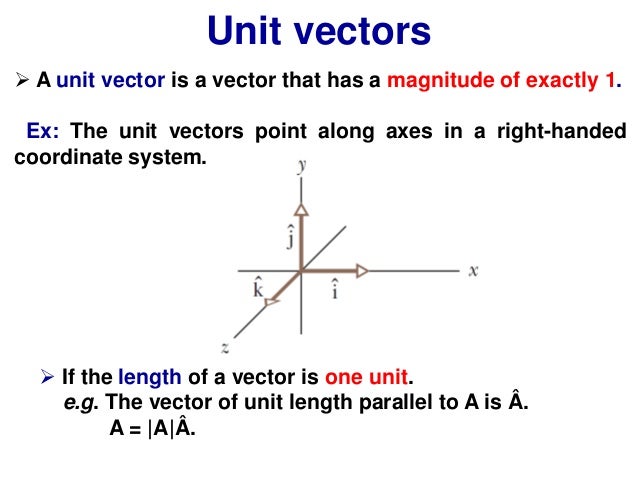
Ba 2a22b21 2bcad 2acbd 2adbc 2a22c21 2cdab 2bdac 2abcd 2a22d21 21513. Here we are applying the graphical rules for adding vectors to construct a triangle. For example the average velocity vector is v d f d o t where d o and d f are the initial and final displacement vectors and t is the time elapsed. Kinematics is a subfield of classical mechanics that describes the motion of points bodies.
Conceptual ideas develop logically and sequentially ultimately leading into the mathematics of the topics. The variables include acceleration a time t displacement d final velocity vf and initial velocity vi. Review of kinematics using vectors physics 3a fall 2001 this is a short summary to review the two main kinematics equations and compare the use of components versus vector diagrams. A2b2c d2bc ad 2acbd 2adbca2bc2d22cdab 2bdac 2abcda2b2c2d2.
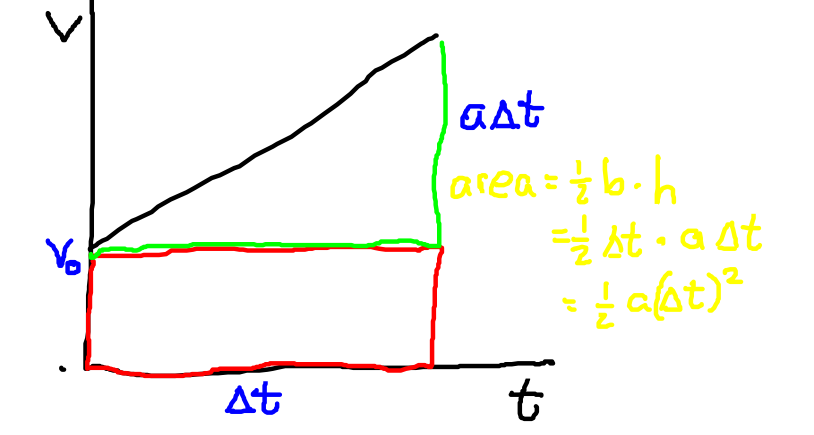
Kinematical equations if acceleration a is constant and t0 0 we get v t v at 0 r t r v at dt 2 0 0 0 or r t r v t at 0 0 1 2 t 37.












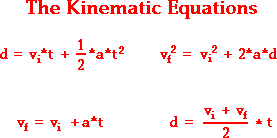







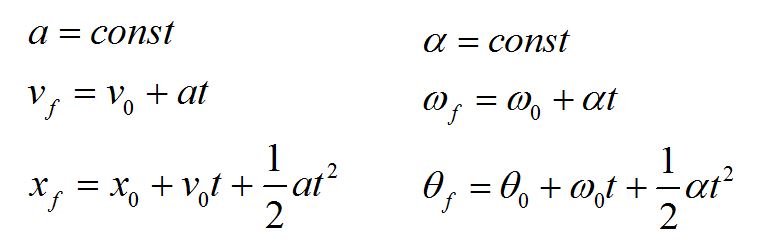





.PNG)