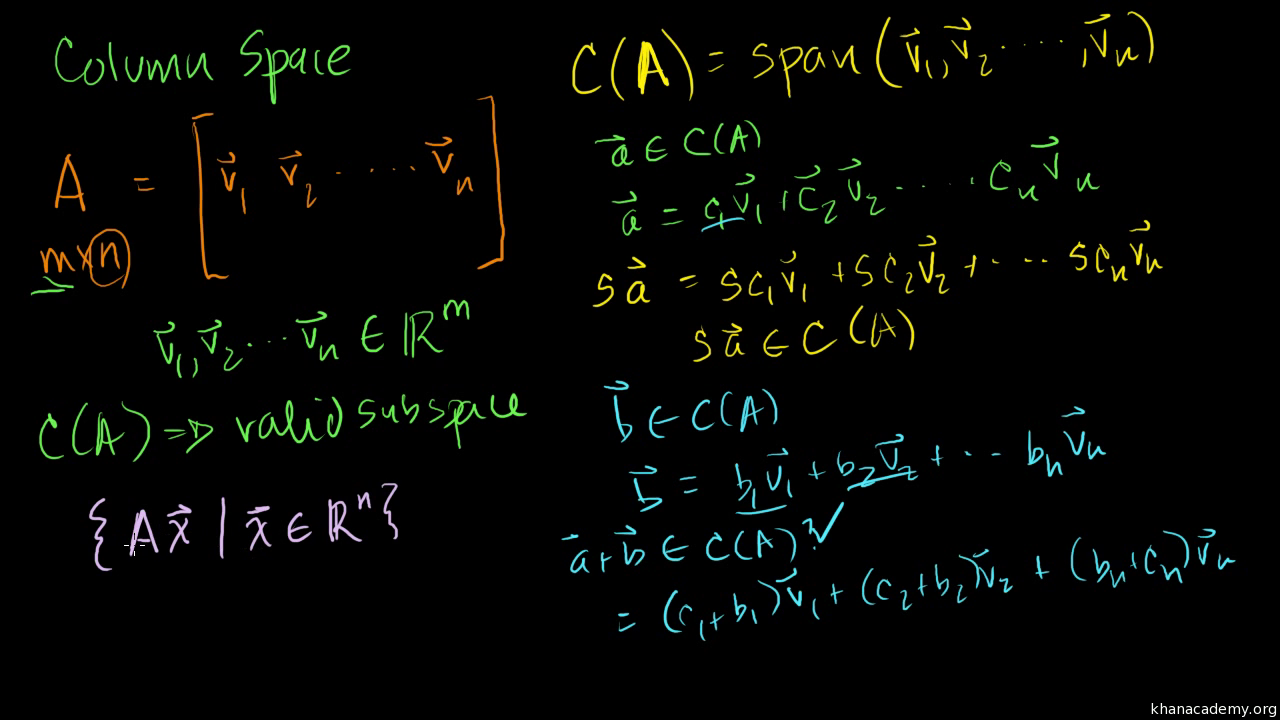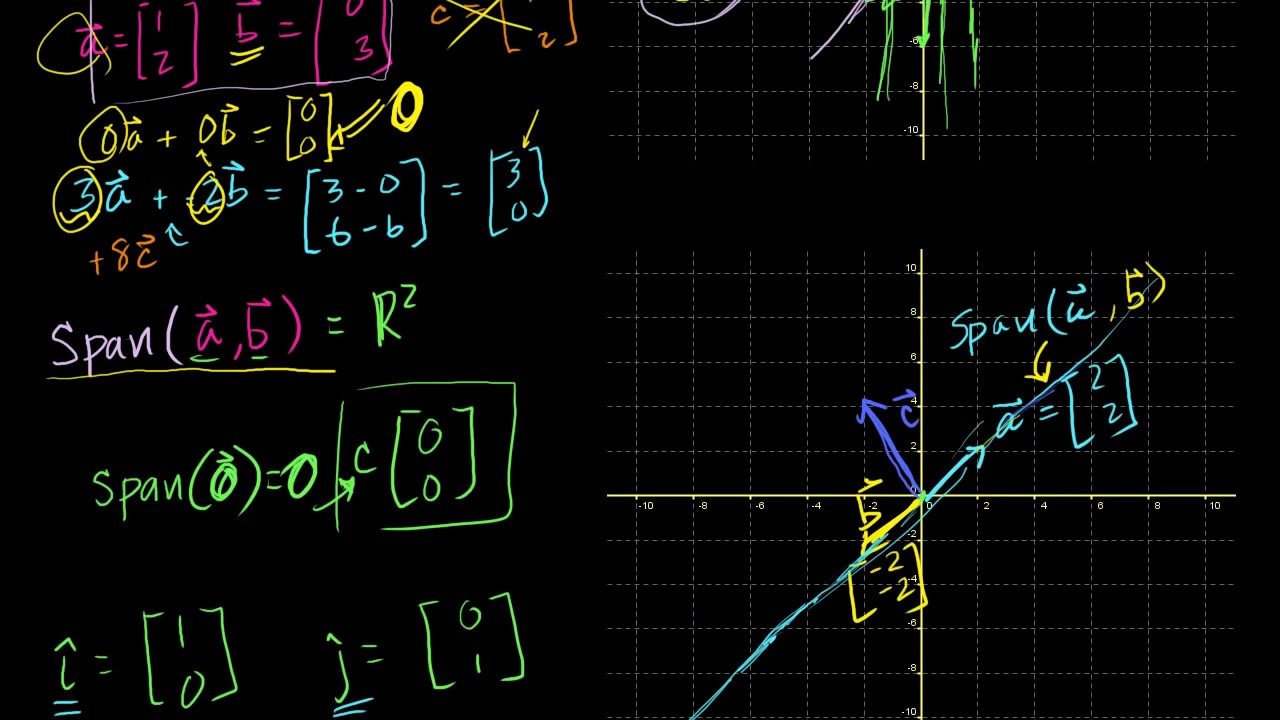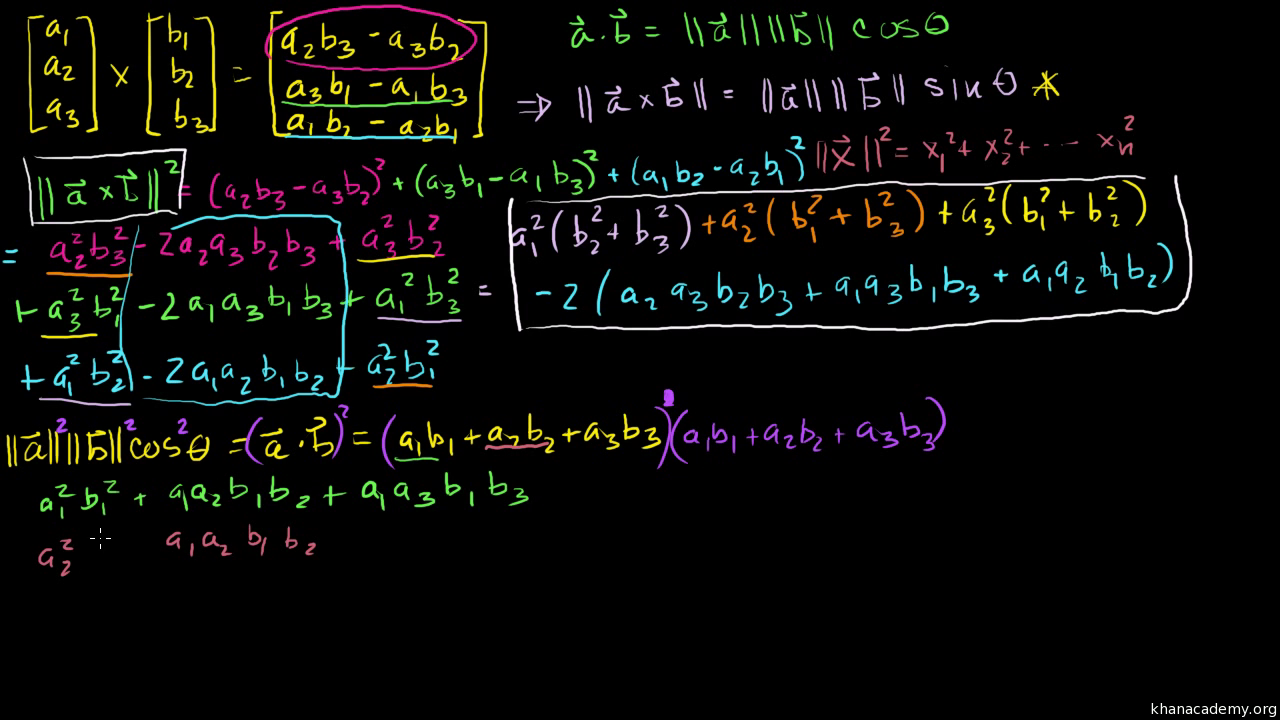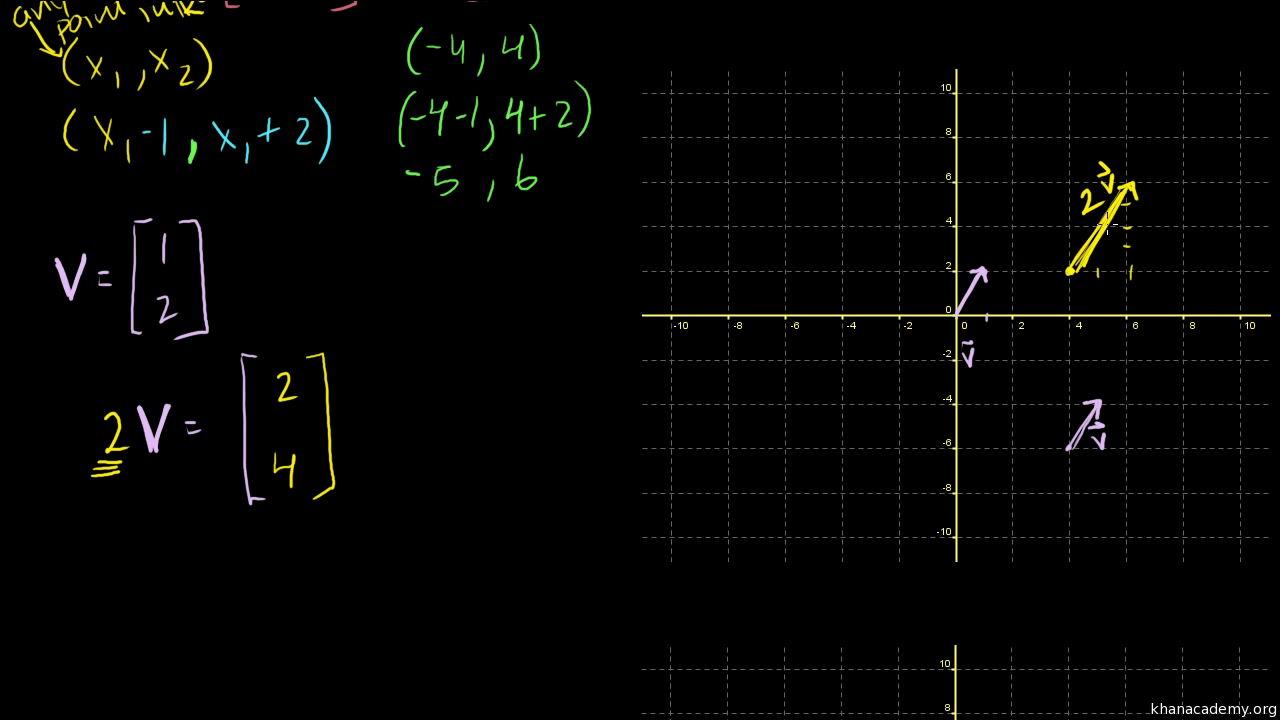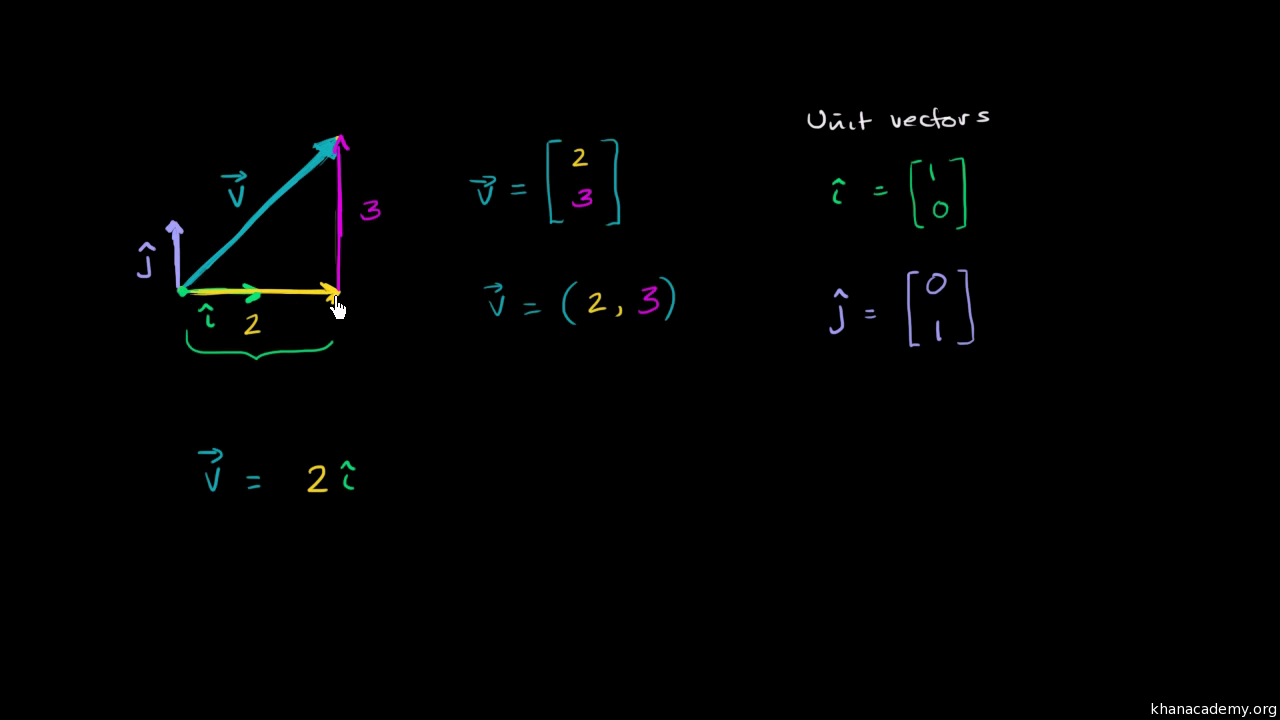Vector Space Axioms Khan Academy

That might make sense.

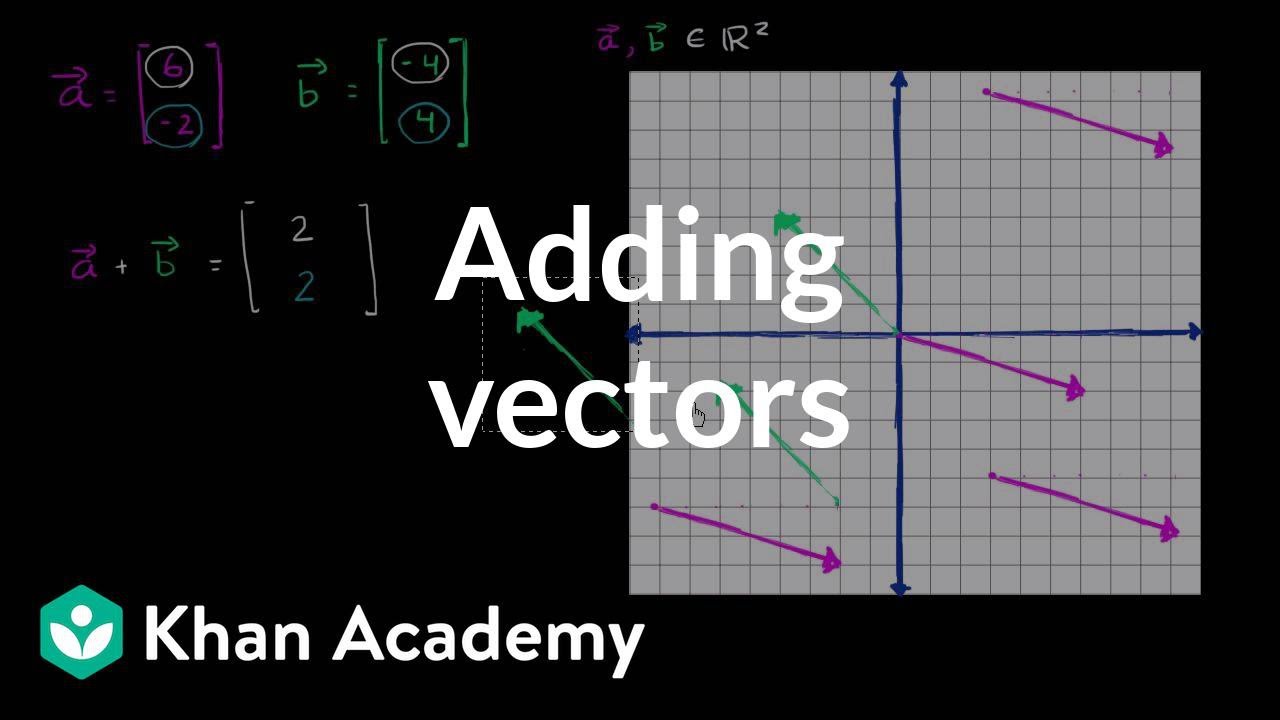
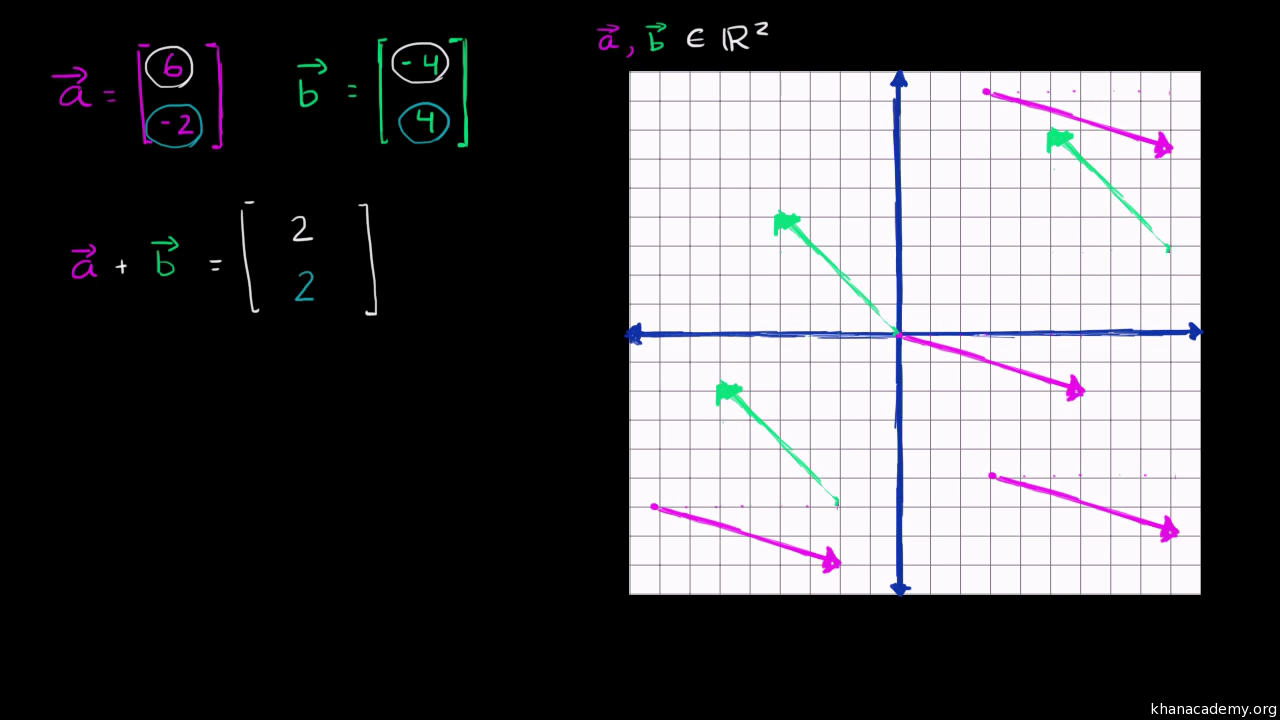
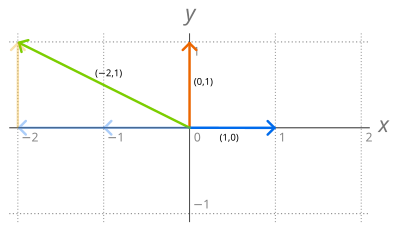
Vector space axioms khan academy. Well lets do something interesting. The scalar scaled up the vector. A real vector space is a set x with a special element 0 and three operations. So this is vector a in standard position right there.

Or it might make an intuition of where that word scalar came from. The axioms must hold for all u v and w in v and for all scalars c and d. Introduction to linear subspaces of rn. And then vector b in standard position is 3 go to the 3 right and then up 1.

Theres also a nice graphical way to add vectors and the two ways will always result in the same vector. The sum of 24 and 15 is 2145 which is 39. If youre seeing this message it means were having trouble loading external resources on our website. To add the vectors x1y1 and x2y2 we add the corresponding components from each vector.

Lets multiply our vector a by a negative number. We let a and b be elements of the field f. Given an element x in x one can form the inverse x which is also an element of x. A vector space is a nonempty set v of objects called vectors on which are defined two operations called addition and multiplication by scalars real numbers subject to the ten axioms below.

Given two elements x y in x one can form the sum xy which is also an element of x. There are ten axioms that define a vector space. Khan academy 833464 views. U v is in v.

U v v u. Heres a concrete example. Lets get our feet wet by thinking in terms of vectors and spaces. In this lecture i introduce the axioms of a vector space and describe what they mean.

Axioms of real vector spaces. It increased its magnitude by 3 without changing its direction. And then vector b in standard position. Axioms for vector spaces.

The scalar when you multiply it it scales up a vector. I then provide several examples of vector spaces.